Троих пиратов спросили сколько монет и сколько алмазов у их друга серая борода

Опубликовано: 17.09.2024

«Кенгуру» — это массовый международный конкурс-игра для школьников под девизом «Математика для всех». Главная цель конкурса — привлечь как можно больше ребят к решению математических задач, показать каждому школьнику, что обдумывание задачи может быть делом живым, увлекательным, и даже веселым!

В 2021 году конкурс «Кенгуру» будет проводиться 18 марта.

«Кенгуру — выпускникам» — это тестирования по математике для учеников 4-х, 9-х и 11-х классов, основная цель которых – независимая проверка учащимися своих знаний по математике и тренировка перед выпускным (переводным) экзаменом. По итогам тестирования каждый участник получит индивидуальную рецензию.

Вопросы и ответы на конкурс Кенгуру для 5-6 класса

Задания на 3 балла

1. Какие из следующих конструкций можно построить из этих 6 кирпичей?

2. Сколько есть пар, в которых дети держат друг друга левыми руками?

3. Если правильно сложить картинки, получится сумма чисел. Чему она равна?

4. 5 фигур на клеточной сетке могут двигаться вправо, влево, вверх и вниз. Какая из них может пройти через ворота G?

5. Перемножили делящиеся на 5 числа от 1 до 100. На сколько нулей оканчивается произведение?

6. На каком из рисунков раскрашена 1/8 часть большого квадрата?

7. Софья хочет написать слово KENGU, используя буквы из коробок. Она может взять только одну букву из каждой коробки. Какую букву Софья должна взять из коробки 4?

Правильный ответ: Г. G

8. У Маши был листок бумаги. Она сложила его пополам, так что две части точно совпали. Потом снова сложила пополам. Она получила фигуру, как на рисунке справа. Какой формы P, Q или R был листок у Маши?

Правильный ответ: Д. любой из P, Q, R

9. Число 5021972970 написано на листке бумаги. Жора дважды разрезает лист и получает три числа. Какую наименьшую сумму он может получить, сложив эти три числа?

Правильный ответ: Б. 3444

10. На карте показаны три автобусные остановки в точках A, B и C. Маршрут от станции А до зоопарка и порта и обратно до А составляет 10 км. Длина маршрута от станции В до парка и зоопарка и обратно до станции В составляет 12 км. Маршрут от станции С до порта и парка и обратно до С составляет 13 км. Также маршрут из зоопарка в парк и порт и обратно в зоопарк имеет протяженность 15 км. Какой самый короткий путь из А в В и С и обратно в А?

Правильный ответ: 18 км

11. 10 одинаковых шариков образуют пирамиду, как показано на рисунке справа. Каждый шарик подписан А, Б, С, D или Е. Каждая буква написана на двух шариках. На картинке показаны стороны (грани) пирамиды. Какая буква соответствует шарику с вопросом?

Правильный ответ: А

12. Мой младший брат закрыл свой четырехзначный велосипедный замок (цифры от 0 до 9) и повернул каждую цифру в одном и том же направлении на одинаковое расстояние так, что получилась комбинация 6348. Какая из комбинаций ниже НЕ может быть кодом замка?

Правильный ответ: В — 4906

13. В коробке было 20 яблок и 20 груш. Влад взял из этой коробке 20 фруктов, Лука взял остальные 20 фруктов. Какое из следующих предложений верно?

Правильный ответ: Г — Влад получил столько же груш, сколько у Луки яблок

14. Точки X и Y соединяет одноколейный железнодорожный путь. Железнодорожная компания хочет, чтобы один поезд отправлялся из Х, и один поезд отправлялся из Y в одно и то же время ежедневно. Двигаясь с постоянной скоростью, поезду требуется 180 минут, чтобы пройти из Х в Y, и 60 минут из Y в Х. Компания хочет построить двойной путь на одном из участков, чтобы избежать аварии. Какой вариант она должна выбрать?

Правильный ответ: Б

15. На картинке справа три шестиугольника с числами в вершинах, но часть чисел невидима. В каждом шестиугольнике сумма чисел в вершинах равна 30. Какое число должно стоять вместо вопроса?

Правильный ответ: Б — 4

16. Три прямоугольника одной высоты расположены как показано справа. Числа в них — их площади в квадратных сантиметрах. Если АВ = 6 см, то какова длина у СD?

Правильный ответ: 8 см

17. На картинке справа 3 шестеренки, каждая с черным зубом. На каком рисунке правильно показали позицию черных зубчиков после полного оборота маленькой шестеренки?

Правильный ответ: А

18. Яблоко и апельсин весят столько же, сколько груша и персик. Яблоко и груша весят меньше апельсина и персика, а груша и апельсин весят меньше яблока и персика. Какой из фруктов самый тяжелый?

Правильный ответ: В — персик

19. Какое наименьшее число квадратов надо дополнительно заштриховать, чтобы вся полученная картинка имела четыре оси симметрии?

Правильный ответ: 21

20. Есть кубик со стороной 7 см. На каждой из его шести граней рисуем по две диагонали красным цветом. Затем нарезаем кубик на маленькие кубики, длина сторон которых составляет 1 см. На скольких маленьких кубиках будет нарисована хотя бы одна красная линия?

Правильный ответ: Б — 62

21. Есть десять троллей и эльфов. Тролли всегда лгут, эльфы всегда говорят правду. Раздали десять жетонов с номерами от 1 до 10, по жетону каждому из них. Когда их спросили о числе на их жетоне, все они назвали число от 1 до 10, и сумма полученных чисел составила 36. Какое наименьшее количество троллей среди них?

Правильный ответ: Б — 3 тролля

22. Прямоугольные двусторонние карты разделены на четыре равные ячейки в каждой из которых нарисованы разные фигуры. Карты можно размещать рядом, только если одинаковые фигуры появляются в соседних ячейках на их общей стороне. Девять карточек образуют прямоугольник, как показано на рисунке. Какая из следующих карт определенно не использовалась для формирования этого прямоугольника?

Правильный ответ: В

23. На каждой полке в общей сложности 64 децилитра яблочного сока. Бутылки бывают трех разных размеров: большие, средние и маленькие. Сколько децилитров яблочного сока содержится в средней бутылке?

Правильный ответ: Г — 10

24. Троих пиратов спросили, сколько монет и сколько алмазов у их друга Серая Борода. Каждый из троих правдиво ответил на один из вопросов, но солгал на другой. Их ответы: «У него 8 монет и 6 алмазов», «У него 7 монет и 4 алмаза», «У него 7 монет и 7 алмазов». Какое общее количество монет и алмазов есть у Серой Бороды?

Правильный ответ: В — 13

Уважаемые посетители, если у Вас есть возможные оставшиеся вопросы, пожалуйста сообщите нам, заранее спасибо. Либо Вы заметили неправильный ответ.

Кенгуру — один из самых популярных конкурсов школьников по математике в мире. Каждый год в нём участвуют более шести миллионов школьников, из них около двух — в России. Каждый желающий, вне зависимости от уровня знания математики, может поучаствовать в конкурсе-игре «Кенгуру».

Сложность заданий делится по возрастным группам: 2 класс, 3-4 классы, 5-6 классы, 7-8 классы и 9-10 классы.

Мы представляем вашему вниманию все ответы на задания для 5-6 классов. Если не согласны с ответом или увидели ошибку, пишите в комментариях.

Кенгуру 2021 все ответы 5-6 класс
1. Какие из следующих конструкций можно построить из этих 6 кирпичей?
2. Сколько есть пар, в которых дети держат друг друга левыми руками?
3. Если правильно сложить картинки, получится сумма чисел.
4. 5 фигур на клеточной сетке могут двигаться вправо, влево, вверх и вниз.
5. Перемножили делящиеся на 5 числа от 1 до 100.
6. На каком из рисунков раскрашена 1/8 часть большого квадрата?
7. Софья хочет написать слово KENGU, используя буквы из коробок. Она может взять только одну букву из каждой коробки.
8. У Маши был листок бумаги. Она сложила его пополам, так что две части точно совпали.
9. Число 5021972970 написано на листке бумаги. Жора дважды разрезает лист и получает три числа.
10. На карте показаны три автобусные остановки в точках A, B и C.
11. 10 одинаковых шариков образуют пирамиду, как показано на рисунке справа.
12. Мой младший брат закрыл свой четырехзначный велосипедный замок (цифры от 0 до 9) и повернул каждую цифру в одном и том же направлении на одинаковое расстояние так, что получилась комбинация 6348.
13. В коробке было 20 яблок и 20 груш. Влад взял из этой коробке 20 фруктов, Лука взял остальные 20 фруктов.
14. Точки X и Y соединяет одноколейный железнодорожный путь.
15. На картинке справа три шестиугольника с числами в вершинах, но часть чисел невидима.
16. Три прямоугольника одной высоты расположены как показано справа.
17. На картинке справа 3 шестеренки, каждая с черным зубом.
18. Яблоко и апельсин весят столько же, сколько груша и персик.
19. Какое наименьшее число квадратов надо дополнительно заштриховать, чтобы вся полученная картинка имела четыре оси симметрии?
20. Есть кубик со стороной 7 см. На каждой из его шести граней рисуем по две диагонали красным цветом.
21. Есть десять троллей и эльфов. Тролли всегда лгут, эльфы всегда говорят правду.
22. Прямоугольные двусторонние карты разделены на четыре равные ячейки в каждой из которых нарисованы разные фигуры.
23. На каждой полке в общей сложности 64 децилитра яблочного сока.
24. Троих пиратов спросили, сколько монет и сколько алмазов у их друга Серая Борода.

Кенгуру 2021 все ответы 5-6 класс

1. Какие из следующих конструкций можно построить из этих 6 кирпичей?

2. Сколько есть пар, в которых дети держат друг друга левыми руками?

3. Если правильно сложить картинки, получится сумма чисел.

4. 5 фигур на клеточной сетке могут двигаться вправо, влево, вверх и вниз.

Какая из них может пройти через ворота G?

5. Перемножили делящиеся на 5 числа от 1 до 100.

На сколько нулей оканчивается произведение?

6. На каком из рисунков раскрашена 1/8 часть большого квадрата?

7. Софья хочет написать слово KENGU, используя буквы из коробок. Она может взять только одну букву из каждой коробки.

Какую букву Софья должна взять из коробки 4?

8. У Маши был листок бумаги. Она сложила его пополам, так что две части точно совпали.

Потом снова сложила пополам. Она получила фигуру, как на рисунке справа.

Какой формы P, Q или R был листок у Маши?

(Д) любой из Р, Q, R.

9. Число 5021972970 написано на листке бумаги. Жора дважды разрезает лист и получает три числа.

Какую наименьшую сумму он может получить, сложив эти три числа?

10. На карте показаны три автобусные остановки в точках A, B и C.

Маршрут от станции А до зоопарка и порта и обратно до А составляет 10 км. Длина маршрута от станции В до парка и зоопарка и обратно до станции В составляет 12 км. Маршрут от станции С до порта и парка и обратно до С составляет 13 км. Также маршрут из зоопарка в парк и порт и обратно в зоопарк имеет протяженность 15 км. Какой самый короткий путь из А в В и С и обратно в А?

11. 10 одинаковых шариков образуют пирамиду, как показано на рисунке справа.

Каждый шарик подписан А, Б, С, D или Е. Каждая буква написана на двух шариках. На картинке показаны стороны (грани) пирамиды. Какая буква соответствует шарику с вопросом?

12. Мой младший брат закрыл свой четырехзначный велосипедный замок (цифры от 0 до 9) и повернул каждую цифру в одном и том же направлении на одинаковое расстояние так, что получилась комбинация 6348.

Какая из комбинаций ниже НЕ может быть кодом замка?

13. В коробке было 20 яблок и 20 груш. Влад взял из этой коробке 20 фруктов, Лука взял остальные 20 фруктов.

Какое из следующих предложений верно?

А) Влад получил как минимум одну грушу

Б) Влад получил столько же яблок, сколько и груш

В) Влад получил столько же груш, сколько Лука

Г) Влад получил столько же груш, сколько у Луки яблок

Д) Влад получил столько же груш ,сколько Лука

Правильный ответ: Г) Влад получил столько же груш, сколько у Луки яблок

14. Точки X и Y соединяет одноколейный железнодорожный путь.

Железнодорожная компания хочет, чтобы один поезд отправлялся из Х, и один поезд отправлялся из Y в одно и то же время ежедневно. Двигаясь с постоянной скоростью, поезду требуется 180 минут, чтобы пройти из Х в Y, и 60 минут из Y в Х. Компания хочет построить двойной путь на одном из участков, чтобы избежать аварии. Какой вариант она должна выбрать?

15. На картинке справа три шестиугольника с числами в вершинах, но часть чисел невидима.

В каждом шестиугольнике сумма чисел в вершинах равна 30. Какое число должно стоять вместо вопроса?

16. Три прямоугольника одной высоты расположены как показано справа.

Числа в них — их площади в квадратных сантиметрах. Если АВ = 6 см, то какова длина у СD?

17. На картинке справа 3 шестеренки, каждая с черным зубом.

На каком рисунке правильно показали позицию черных зубчиков после полного оборота маленькой шестеренки?

18. Яблоко и апельсин весят столько же, сколько груша и персик.

Яблоко и груша весят меньше апельсина и персика, а груша и апельсин весят меньше яблока и персика. Какой из фруктов самый тяжелый?

Д) невозможно определить

19. Какое наименьшее число квадратов надо дополнительно заштриховать, чтобы вся полученная картинка имела четыре оси симметрии?

20. Есть кубик со стороной 7 см. На каждой из его шести граней рисуем по две диагонали красным цветом.

Затем нарезаем кубик на маленькие кубики, длина сторон которых составляет 1 см. На скольких маленьких кубиках будет нарисована хотя бы одна красная линия?

21. Есть десять троллей и эльфов. Тролли всегда лгут, эльфы всегда говорят правду.

Раздали десять жетонов с номерами от 1 до 10, по жетону каждому из них. Когда их спросили о числе на их жетоне, все они назвали число от 1 до 10, и сумма полученных чисел составила 36. Какое наименьшее количество троллей среди них?

22. Прямоугольные двусторонние карты разделены на четыре равные ячейки в каждой из которых нарисованы разные фигуры.

Карты можно размещать рядом, только если одинаковые фигуры появляются в соседних ячейках на их общей стороне. Девять карточек образуют прямоугольник, как показано на рисунке. Какая из следующих карт определенно не использовалась для формирования этого прямоугольника?

23. На каждой полке в общей сложности 64 децилитра яблочного сока.

Бутылки бывают трех разных размеров: большие, средние и маленькие.

Сколько децилитров яблочного сока содержится в средней бутылке?

24. Троих пиратов спросили, сколько монет и сколько алмазов у их друга Серая Борода.

Каждый из троих правдиво ответил на один из вопросов, но солгал на другой. Их ответы: «У него 8 монет и 6 алмазов», «У него 7 монет и 4 алмаза», «У него 7 монет и 7 алмазов». Какое общее количество монет и алмазов есть у Серой Бороды?

Кенгуру 2021 ответы и задания для 5-6 класса
Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Задание 6
Задание 7
Задание 8
Задание 9
Задание 10
Задание 11
Задание 12
Задание 13
Задание 14
Задание 15
Задание 16
Задание 17
Задание 18
Задание 19
Задание 20
Задание 21
Задание 22
Задание 23
Задание 24

Кенгуру 2021 ответы и задания для 5-6 класса

Очередной конкурс «Кенгуру» состоится 18 марта 2021 года. Конкурс проходит один раз в год — в третий четверг марта, проводится он обязательно в школе, подробная информация по ссылке на официальную страницу организатора конкурса: Кенгуру
Ниже представляем первые 11 заданий Кенгуру для 5-6 класса и ответы к ним, обсуждаем остальные задания и ответы в комментариях.

Задачи на 3 балла

Задание 1

Какие из следующих конструкций можно построить из этих 6 кирпичей?

Наш вариант ответа: (Г)

Задание 2

Сколько есть пар, в которых дети держат друг друга левыми руками?

Наш вариант ответа: (А) 1

Задание 3

Если правильно сложить картинки, получится сумма чисел. Чему она равна?

Наш вариант ответа: (Б) 32

Задание 4

5 фигур на клеточной сетке могут двигаться вправо, влево, вверх и вниз. Какая из них может пройти через ворота G?

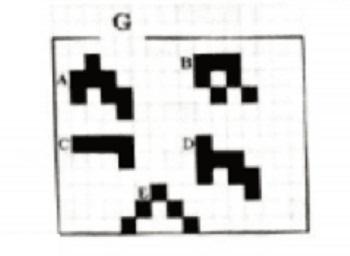
Наш вариант ответа: (Б) В

Задание 5

Перемножили делящиеся на 5 числа от 1 до 100. На сколько нулей оканчивается произведение?

Наш вариант ответа: В

Задание 6

На каком из рисунков раскрашена 1/8 часть большого квадрата?

Наш вариант ответа: (Г)

Задание 7

Софья хочет написать слово KENGU, используя буквы из коробок. Она может взять только одну букву из каждой коробки. Какую букву Софья должна взять из коробки 4?

Наш вариант ответа: (Г) G

Задание 8

У Маши был листок бумаги. Она сложила его пополам, так что две части точно совпали.

Потом снова сложила пополам. Она получила фигуру, как на рисунке справа. Какой формы P, Q или R был листок у Маши?

Наш вариант ответа: (А) только Р

Задачи на 4 балла

Задание 9

Число 5021972970 написано на листке бумаги. Жора дважды разрезает лист и получает три числа. Какую наименьшую сумму он может получить, сложив эти три числа?

Наш вариант ответа: (Б) 3444

Задание 10

На карте показаны три автобусные остановки в точках A, B и C. Маршрут от станции А до зоопарка и порта и обратно до А составляет 10 км. Длина маршрута от станции В до парка и зоопарка и обратно до станции В составляет 12 км. Маршрут от станции С до порта и парка и обратно до С составляет 13 км. Также маршрут из зоопарка в парк и порт и обратно в зоопарк имеет протяженность 15 км. Какой самый короткий путь из А в В и С и обратно в А?

Наш вариант ответа: (Б) 20 км

Задание 11

10 одинаковых шариков образуют пирамиду, как показано на рисунке справа.

Наш вариант ответа: (А) A

Задание 12

Мой младший брат закрыл свой четырехзначный велосипедный замок (цифры от 0 до 9) и повернул каждую цифру в одном и том же направлении на одинаковое расстояние так, что получилась комбинация 6348. Какая из комбинаций ниже НЕ может быть кодом замка?

Наш вариант ответа: (В) 4906

Задание 13

В коробке было 20 яблок и 20 груш. Влад взял из этой коробке 20 фруктов, Лука взял остальные 20 фруктов. Какое из следующих предложений верно?

Наш вариант ответа: (Г) Влад получил столько же груш, сколько у Луки яблок

Задание 14

Точки X и Y соединяет одноколейный железнодорожный путь. Железнодорожная компания хочет, чтобы один поезд отправлялся из Х, и один поезд отправлялся из Y в одно и то же время ежедневно. Двигаясь с постоянной скоростью, поезду требуется 180 минут, чтобы пройти из Х в Y, и 60 минут из Y в Х. Компания хочет построить двойной путь на одном из участков, чтобы избежать аварии. Какой вариант она должна выбрать?

Наш вариант ответа: (Б)

Задание 15

На картинке справа три шестиугольника с числами в вершинах, но часть чисел невидима. В каждом шестиугольнике сумма чисел в вершинах равна 30. Какое число должно стоять вместо вопроса?

Наш вариант ответа: (Б) 4

Задание 16

Три прямоугольника одной высоты расположены как показано справа. Числа в них — их площади в квадратных сантиметрах. Если АВ = 6 см, то какова длина у СD?

Наш вариант ответа: (В) 8 см

Задание 17

На картинке справа 3 шестеренки, каждая с черным зубом. На каком рисунке правильно показали позицию черных зубчиков после полного оборота маленькой шестеренки?

Наш вариант ответа: (А)

Задание 18

Яблоко и апельсин весят столько же, сколько груша и персик. Яблоко и груша весят меньше апельсина и персика, а груша и апельсин весят меньше яблока и персика. Какой из фруктов самый тяжелый?

Наш вариант ответа: (Г) груша

Задание 19

Какое наименьшее число квадратов надо дополнительно заштриховать, чтобы вся полученная картинка имела четыре оси симметрии?

Наш вариант ответа: (В) 12

Задание 20

Есть кубик со стороной 7 см. На каждой из его шести граней рисуем по две диагонали красным цветом. Затем нарезаем кубик на маленькие кубики, длина сторон которых составляет 1 см. На скольких маленьких кубиках будет нарисована хотя бы одна красная линия?

Наш вариант ответа: (Б) 62

Задание 21

Есть десять троллей и эльфов. Тролли всегда лгут, эльфы всегда говорят правду. Раздали десять жетонов с номерами от 1 до 10, по жетону каждому из них. Когда их спросили о числе на их жетоне, все они назвали число от 1 до 10, и сумма полученных чисел составила 36. Какое наименьшее количество троллей среди них?

Наш вариант ответа: (Б) 3

Задание 22

Прямоугольные двусторонние карты разделены на четыре равные ячейки в каждой из которых нарисованы разные фигуры. Карты можно размещать рядом, только если одинаковые фигуры появляются в соседних ячейках на их общей стороне. Девять карточек образуют прямоугольник, как показано на рисунке. Какая из следующих карт определенно не использовалась для формирования этого прямоугольника?

Наш вариант ответа: (Г)

Задание 23

На каждой полке в общей сложности 64 децилитра яблочного сока. Бутылки бывают трех разных размеров: большие, средние и маленькие. Сколько децилитров яблочного сока содержится в средней бутылке?

Наш вариант ответа: (Г) 10

Задание 24

Троих пиратов спросили, сколько монет и сколько алмазов у их друга Серая Борода. Каждый из троих правдиво ответил на один из вопросов, но солгал на другой. Их ответы: «У него 8 монет и 6 алмазов», «У него 7 монет и 4 алмаза», «У него 7 монет и 7 алмазов». Какое общее количество монет и алмазов есть у Серой Бороды?

Наш вариант ответа: (В) 13

с 18 по 23 января 2021 года уже проводилась Олимпиада Кенгуру для выпускных 4, 9 и 11 класса

Задача

Несколько пиратов делят добытое сокровище. У каждого из них свои представления о прекрасном, поэтому одну и ту же долю разные пираты могут оценивать по-разному. Будем считать, что сокровище можно делить на сколь угодно маленькие части.

1) Пират доволен, если по итогам дележа ему досталось не меньше 1/n добычи по его собственной оценке (n — число пиратов). Как действовать пиратам, чтобы все они были довольны результатом, если их двое; трое? Ответьте на этот вопрос в общем случае.
2) Пусть теперь пираты завистливы: каждый доволен, только если он считает, что получил не меньше любого другого пирата. Как троим завистливым пиратам поделить сокровище и остаться довольными?

Подсказка 1

Прежде всего, уточним, что хотя вкусы у пиратов и разные, но здравого смысла они не лишены и ни один из них не оценит заведомо меньшую долю выше, чем заведомо большую (например, если из какой-то части сокровищ что-то отложили, то все пираты понимают, что эта часть стала меньше).

Двоим пиратам разделить добычу между собой легко: сначала один разделит ее пополам (в соответствии со своими предпочтениями), а затем второй выберет из двух половин ту, которая ему больше нравится. Это решение простое, но может быть не очень понятно, как его перенести на случай трех и более пиратов.

Для этого сформулируем ту же идею по-другому. Первый пират разделит сокровище пополам, а затем выберет одну из половин и спросит у второго, не возражает ли тот против такого выбора. Если тот не против, то первый заберет свою половину и оба будут довольны, а если второй против, то первый предложит второму отсыпать лишнее и забрать оставшееся.

Подсказка 2

С завистливыми пиратами, если их больше двух, все сложнее (когда их двое, то работает решение из подсказки 1). Но начинать с чего-то надо, поэтому одному из них придется поделить добычу на три части. Другие двое будут уверены, что его деление, конечно же, несправедливое. Понять, как действовать дальше, поможет частный случай, когда второй пират считает, что две из трех частей равны друг другу.

Решение

Сначала закончим решение задачи для независтливых пиратов, развивая идею из первой подсказки. Пусть их будет трое или больше (то есть n > 2). Действовать им нужно так. Сначала один из них — будем называть его П₁ — отмеряет себе 1/n от добычи (по своим понятиям). Затем он должен по очереди спросить всех остальных, согласны ли они с тем, что отмерено не больше 1/n. Если никто не возразит, то П₁ забирает свою долю. Он доволен, а всем остальным тоже нет повода для расстройства: каждый из них считает, что П₁ отмерил себе меньше 1/n, поэтому им при справедливом дележе остатка достанется даже больше этой доли. Если же кто-то (назовем его П₂) возразит, то П₁ попросит этого несогласного отсыпать лишнее и отдаст ему долю. После этого уже П₂ будет продолжать опрос. Всех, кто уже был опрошен, заново спрашивать не нужно — доля только уменьшилась, и они на нее претендовать не будут. Если появится еще один несогласный (П₃), то он отсыпет лишнее у П₂ и заберет оставшееся сокровище себе. Этот процесс рано или поздно закончится, потому что пиратов конечное число, а число неопрошенных всё время уменьшается. Последний, кто отсыпал лишнее, должен будет забрать долю себе и больше не будет участвовать в дележе. Таким образом, гарантированно получается один довольный пират, а все остальные уверены, что получат не меньше 1/n от всего сокровища.

Оставшиеся n − 1 пиратов повторяют описанную в предыдущем абзаце процедуру, пока всё сокровище не будет поделено между ними.

Теперь разберемся с тремя завистливыми пиратами. Нетрудно понять, почему в этом случае не работает описанный выше способ: после того как первый пират получит свою «треть» сокровища, двое других как-то разделят остаток между собой, но вот первого результат этого раздела может и не устроить.

Допустим, первый пират разделил сокровище на, как он считает, три равноценные части: А, Б и В. Предложим второму расположить эти части по убыванию ценности. Можно считать, что порядок такой: А — самая ценная часть, В — самая дешевая, а Б имеет промежуточную ценность. «Неравенства» здесь нестрогие — части могут иметь одинаковую ценность. Если по мнению второго пирата А = Б, то дальше всё просто: третий выбирает свою долю, у второго в любом случае остается возможность забрать одну из двух более ценных частей, а первый и так считал, что они все три равноценные, поэтому оставшаяся часть его устроит.

А как быть, если по мнению второго А > Б? Тогда попросим его отложить «лишнее» А₁ из части А, чтобы остаток А₂ уравнялся с частью Б. Три части — А₂, Б и В — пираты смогут распределить между собой, чтобы все были довольны. Это делается аналогично случаю А = Б с одним уточнением: если третий забрал часть В, то второго попросим не брать часть Б (ему-то неважно, что брать — часть Б или «похудевшую» часть А), чтобы первый пират не расстроился. Остается поделить излишек А₁. Заметим, что первый точно не будет завидовать тому, кто взял себе А₂, потому что туда не получится добавить больше, чем А₁, то есть больше части А по мнению первого точно не получится. Пусть, для определенности, часть А₂ досталась второму пирату. Тогда попросим третьего поделить излишек А₁ на три равные части, а второго — выбрать из них ту, которая ему больше понравится. Затем первый выберет одну из двух оставшихся частей, а последняя достанется третьему. В итоге все три пирата будут довольны и не будут никому завидовать.

Послесловие

Скорее всего, подобную задачу о честном дележе впервые сформулировал Гуго Штейнгауз (Hugo Steinhaus) еще во время Второй мировой войны. В дальнейшем возникло большое множество задач о справедливом дележе (см. Fair division), в которых варьируются разные параметры: тип «сокровищ» (допускает ли оно непрерывное деление на сколь угодно малые части или его можно разделить лишь на конечное количество частей), количество «пиратов» и их предпочтения, наличие и отсутствие зависти и другие. С точки зрения математики эти задачи относятся к теории меры, теории игр, теории алгоритмов. Некоторые из них являются хорошими моделями для реальных ситуаций, поэтому важны, например, и для экономики. Рассмотренные нами две задачи в англоязычной литературе обычно называют задачами о делении пирога (см. Fair cake-cutting). Решение второй задачи с произвольным числом пиратов можно найти в статье С. Брамса и А. Тейлора An Envy-Free Cake Division Protocol.

Приведу еще одно рассуждение, которое помогает решить нашу первую задачу (на самом деле, оно очень близко к разобранному решению, но гораздо короче). Удобно считать, что пираты делят мешок золотого песка. Один из них начинает отсыпать кучку и сыпет до тех пор, пока кто-нибудь не крикнет «Стоп!» (считая, что отсыпалась как раз доля 1/n). Тот, кто крикнул, забирает кучку себе и выбывает из процесса, а остальные продолжают дальше.

А в завершение расскажу об удивительном (хотя и длинном) решении, основанном на одном комбинаторном факте, который, казалось бы, вообще никак не связан с обсуждаемыми вопросами. Этот факт называется леммой Шпернера и формулируется так:

Дан треугольник, вершины которого покрашены в три цвета. Рассмотрим произвольную триангуляцию этого треугольника. Вершины этой триангуляции покрасим в те же три цвета с единственным условием: вершины триангуляции, которые попали на сторону исходного треугольника, можно красить только в цвет одного из концов этой стороны. Тогда в триангуляции обязательно найдется треугольник с вершинами всех трех цветов.

Чтобы применить эту лемму к задаче о дележе, нужно немного подготовиться. Исключительно для наглядности предположим, что сокровище, которое делят трое пиратов, — это длинная золотая цепь с мелкими звеньями. Примем длину этой цепи за 1 и будем считать, что цепь вытянута в горизонтальный отрезок. Любое разделение этой цепи можно описать парой чисел x и y, обозначающих места, в которых нужно разрезать цепь, чтобы она распалась на три части: x — место первого разреза, y — место второго (считаем, что разрезы могут совпадать — тогда кому-то достается «пустой» кусок цепи, то есть не достается ничего). Тогда выполняются неравенства 0 ≤ x ≤ y ≤ 1. На декартовой плоскости эти неравенства задают треугольник, ограниченный прямыми x = 0, y = 1, y = x. Обратите внимание, что у нас уже появился треугольник! Обозначим его Т. Каждая точка в этом треугольнике задает разделение цепи. Например, точка с координатами (1/3, 2/3) соответствует делению на три равных куска, а точка с координатами (1/2, 1/2) — такому делению: половина, «пустой» кусок, еще половина. Вершины исходного треугольника Т имеют координаты (0, 0), (0, 1), (1, 1) и дают «вырожденные» разрезания, в которых получается только один непустой кусок. Например, вершине (0, 0) соответствует такое разделение: первые два куска пустые, а третий кусок — это вся цепь.

Триангулируем треугольник Т и введем раскраску вершин триангуляции следующим образом. Сначала рядом c этими вершинами напишем имена пиратов так, чтобы рядом с вершинами каждого треугольничка стояли все три имени (поскольку мы вольны в выборе триангуляции, то выберем такую, чтобы это было возможно; а вы придумайте триангуляцию, вершины которой так подписать не получится). Можно сказать, что у каждой вершины триангуляции есть владелец — пират, чье имя написано рядом с вершиной. Пройдем по всем вершинам и спросим их владельцев, какой (по порядку) из кусков соответствующих разделений цепи они бы выбрали себе: левый, средний или правый. В качестве цвета используем характеристики «выбор левого куска», «выбор среднего куска», «выбор правого куска», их как раз три. Убедитесь, что такая «раскраска», несмотря на всю странность, удовлетворяет условиям леммы Шпернера (а именно, что вершины триангуляции, попавшие на стороны исходного треугольника, будут покрашены в цвет одного из концов своей стороны). Тогда, по лемме, обязательно найдется треугольничек, вершины которого будут покрашены в разные цвета. Этот треугольничек можно снова триангулировать, причем так же, как и исходный треугольник. Вершины триангуляции можно покрасить в те же самые три «цвета» и получить еще один, уже совсем маленький, треугольничек с вершинами всех трех цветов. Продолжая этот процесс, получим последовательность вложенных треугольников, которая сходится к одной точке (это двумерный аналог принципа вложенных отрезков). Эта точка и дает нужное разделение, потому что каждый из пиратов выберет свой кусок цепи. Более того, это разделение подойдет и завистливым пиратам.

При подготовке этой задачи были использованы материалы 11-й Летней конференции Турнира городов (см. статью И. Иванова-Погодаева, А. Канель-Белова, С. Кублановского и А. Малистова «Задача о разбойниках» в книге Н. Константинова и Б. Френкина «Летние конференции Турнира городов. Избранные материалы. Выпуск 1»).

Это задача № 19 – самая сложная в вариантах ЕГЭ Профильного уровня.

Надеюсь, что у вас есть и то, и другое. Я буду вашим проводником!

Пираты нашли сундук с сокровищами, в котором было 60 монет достоинством 1 дукат и 60 монет достоинством 5 дукатов.
а) Получится ли поделить все деньги поровну между 18 пиратами (каждому должно достаться целое число монет, сдачи и размена ни у кого из пиратов нет)?
б) Получится ли поделить все деньги поровну между 40 пиратами (каждому должно достаться целое число монет, сдачи и размена ни у кого из пиратов нет)?
в) При каком наибольшем количестве пиратов капитану всегда удастся поделить монеты между ними, каким бы способом ему ни захотелось это сделать (возможно, кому-то из пиратов будет полагаться 0 монет)?

Смело начнем с первого пункта задачи. И сразу получим ответ! Считайте, что вы только начали копать в выбранном месте – и тут же нашли первую золотую монетку, то есть 1 балл за пункт (а)!

а) Получится ли поделить все деньги поровну между 18 пиратами (каждому должно достаться целое число монет, сдачи и размена ни у кого из пиратов нет)?

Да, получится. Каждый пират получит по 20 дукатов. Потому что всего в сундуке дукатов, и 360 отлично делится на 18.

Например, дележка может происходить следующим образом:

– Сначала раздаем все монеты по 5 дукатов. Ровно 15 пиратов получат по 4 таких монеты каждый, то есть по 20 дукатов, а оставшиеся 3 пирата получают по 20 дукатов монетами по 1 дукату.

Главное – чтобы пираты не перессорились и не укокошили друг друга во время раздачи монет. Но это уже проблема капитана пиратов, а не наша.

А мы продолжим нашу «добычу баллов» за задачу 19.

б) Получится ли поделить все деньги поровну между 40 пиратами (каждому должно достаться целое число монет, сдачи и размена ни у кого из пиратов нет)?

Нет, не получится. Если всего 40 пиратов, то каждый из них собирается получить 360 : 40 = 9 дукатов. Однако 9 не делится на 5 нацело. При делении 9 на 5 мы получаем в остатке 4. Это значит, что каждому пирату придется выдать не менее 4 монет по 1 дукату.

Но такого количества монет по 1 дукату в сундуке нет. Предположив, что 40 пиратов смогут разделить сокровище поровну, получаем противоречие с условием.

Что-то подозрительно легко достались нам первые 2 балла. Но 2 монеты – это еще не клад. Копаем дальше?

в) При каком наибольшем количестве пиратов капитану всегда удастся поделить монеты между ними, каким бы способом ему ни захотелось это сделать (возможно, кому-то из пиратов будет полагаться 0 монет)?

…Именно здесь потерпели поражение многие из тех «кладоискателей», которые опубликовали в интернете решения этой задачи. «В условии ошибка!» - заявляли они. – «Здесь клада нет! Дайте нам другую карту!»

Разберемся с условием задачи.

Вам тоже показалось, что количество пиратов может быть каким угодно? Что мы можем увеличивать его хоть до тысячи чертей, просто добавляя пиратов, которым, согласно условию, будет полагаться 0 монет?

Однако не все так просто.

Предположим, что в команде 40 пиратов. Конечно, капитан может тайно присвоить все 360 дукатов, нейтрализовать с помощью бочки рома остальных пиратов (получивших в итоге по 0 монет), удачно скрыться от них и начать новую, умеренную и добропорядочную жизнь. Однако условие задачи в этом случае не выполнено.

По условию, пиратов должно быть столько, чтобы капитан смог «поделить монеты между ними, каким бы способом ему ни захотелось это сделать». Какой же способ для капитана будет самым трудным?

Очевидно, такой, при котором ему не хватит монет достоинством в 1 дукат. Например, поделить 360 дукатов между 40 пиратами поровну не получится. Это доказано в пункте (б).

Вот в чем разница! На вопрос: «Существует ли в этой задаче какой-нибудь способ поделить 360 монет между 40 пиратами?» ответ: «Да». А на вопрос: «Можно ли в условиях задачи поровну поделить 360 монет между 40 пиратами?» – ответ: «Нет».

В пункте (в) речь идет именно о том, чтобы поделить деньги между пиратами любым возможным способом. Лишь бы в сумме получилось 60 монет по 5 дукатов и 60 монет по 1 дукату, и каждый пират получил целое количество дукатов.

Пусть пиратов 15. Даже если деньги распределены так, что каждому из 15 пиратов придется выдать по 4 монеты в 1 дукат, мы сможем это сделать, имея таких монет. Да, похоже, задача составлена по мотивам песни из детской книги «Остров сокровищ»: «15 человек на сундук мертвеца…»

Если пиратов 17, то мы можем подобрать такое распределение денег, что раздать их в условиях задачи будет невозможно. Например, капитан захотел каждому из 16 членов своей команды выдать по 4 дуката, а себе забрать остальное. Сделать этого он не сможет: у него не найдется монет по 1 дукату.

– Значит, ответ: 15?

– Не спешите! Мы еще не проверили, что же будет в случае 16 пиратов.

На первый взгляд кажется, что и для 16 пиратов можно подобрать такое распределение денег, что капитан не сможет их раздать. Например, поделить нацело 360 монет на 16 пиратов невозможно. Но это и не требуется по условию. Проверим, сможет ли капитан раздать любым способом все 60 монет по 5 дукатов и 60 монет по 1 дукату, так что каждый пират получит целое количество дукатов.

Предположим, что все пираты вместе с капитаном построились в одну шеренгу. Пусть i – порядковый номер пирата в этой шеренге: первый, второй, третий, i-тый… Да, математики говорят именно так: i-тый.

Пусть каждый пират получает в результате сумму денег, равную

Пусть – остаток от деления суммы, полученной i-тым пиратом, на 5. Тогда

Каждый пират получил некоторую сумму кратную 5, и еще остаток от деления на 5, который равен и может быть выдан только монетами по 1 дукату.

Очевидно, что самый сложный для капитана случай – когда остатки от деления всех на 5 равны 4, то есть все равны 4.

Действительно, тогда сумма остатков и у капитана не хватит монет по 1 дукату.

– Значит, все-таки 16 пиратов не смогут разделить деньги, и ответ в пункте (в) – пятнадцать?

– Не спешите! Проверим, возможен ли такой случай, когда все остатки от деления на 5, то есть все равны 4. Сложим все и все Очевидно, что сумма всех равна 360 (общее количество дукатов). В математике это записывается так:

Сумму всех остатков от деления на 5 обозначим R.

360 = 5 N + R, где N – сумма всех

Но тогда R = 360 – 5N.

Правая часть этого уравнения делится на 5. Значит, сумма всех остатков R делится на 5.

Очевидно, для любого распределения монет и при этом R делится на 5.

Значит, Прекрасно! У капитана не будет недостатка в монетах по 1 дукату: их понадобится не больше 60, и в случае, если пиратов 16, трудностей не должно быть.

Как вы думаете – решение задачи закончено или чего-то не хватает?

Конечно, не закончили! Осталось непонятно, как же все-таки нужно раздавать дукаты. С каких монет начинать?

Будем действовать следующим образом.

Сначала вычислим остатки от деления всех на 5. Раздадим эти остатки монетами по 1 дукату. Мы выяснили, что это сделать можно, потому что сумма всех остатков

Оставшаяся сумма кратна 5. Раздаем все 5-дукатные монеты и после этого (если остались) монеты по 1 дукату.

Окончательный ответ: 16.

Мой полный курс по задаче 19 Профильного ЕГЭ по математике – здесь

Читайте также: