Когда кос меняется на синус

Опубликовано: 17.09.2024

Формулы приведения ! Они относятся к разделу «тригонометрия» в математике. Суть их заключается в приведении тригонометрических функций углов к более «простому» виду. О важности их знания написать можно много. Этих формул аж 32 штуки!

Не пугайтесь, учить их не надо, как и многие другие формулы в курсе математики. Лишней информацией голову забивать не нужно, необходимо запоминать «ключики» или законы, и вспомнить или вывести нужную формулу проблемой не будет. Кстати, когда я пишу в статьях «… нужно выучить. » – это значит, что действительно, это необходимо именно выучить.

Если вы с формулами приведения не знакомы, то простота их вывода вас приятно удивит – есть «закон», при помощи которого это легко сделать. И любую из 32 формул вы напишите за 5 секунд.

*А тем, кто хочет набить руку решая задачи, вот здесь разобраны 22 примера от простых до самых сложных.

Перечислю лишь некоторые задачи, типы которых возможны на экзамене, где без знания этих формул есть большая вероятность потерпеть фиаско в решении. Например:

– задачи на решение прямоугольного треугольника, где речь идёт о внешнем угле, да и задачах на внутренние углы некоторые из этих формул тоже необходимы.

– задачи на вычисление значений тригонометрических выражений; преобразования числовых тригонометрических выражений; преобразования буквенных тригонометрических выражений.

– задачи на касательную и геометрический смысл касательной, требуется формула приведения для тангенса, а также другие задачи.

– стереометрические задачи, по ходу решения не редко требуется определить синус или косинус угла, который лежит в пределах от 90 до 180 градусов.

И это лишь те моменты, которые касаются ЕГЭ. А в самом курсе алгебры есть множество задач, при решении которых, без знания формул приведения просто не обойтись.

Так что же к чему приводится и как оговоренные формулы упрощают для нас решение задач?

Например, вам нужно определить синус, косинус, тангенс или котангенс любого угла от 0 до 450 градусов:

угол альфа лежит пределах от 0 до 90 градусов

Итак, необходимо уяснить «закон», который здесь работает:

1. Определите знак функции в соответствующей четверти.

2. Запомните следующее:

функция изменяется на кофункцию

функция на кофункцию не изменяется

Что означает понятие — функция изменяется на кофункцию?

Ответ: синус меняется на косинус или наоборот, тангенс на котангенс или наоборот.

Теперь по представленному закону запишем несколько формул приведения самостоятельно:

Данный угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:

Угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Меняем функцию на кофункцию, так как у нас 270 градусов, значит:

Угол лежит в первой четверти, синус в первой четверти положителен. Не меняем функцию на кофункцию, так как у нас 360 градусов, значит:

Вот вам ещё дополнительное подтверждение того, что синусы смежных углов равны:

Угол лежит во второй четверти, синус во второй четверти положителен. Не меняем функцию на кофункцию, так как у нас 180 градусов, значит:

Проработайте мысленно или письменно каждую формулу, и вы убедитесь, что ничего сложного нет.

В статье на решение прямоугольного треугольника был отмечен такой факт – синус одного острого угла в прямоугольном треугольнике равен косинусу другого острого угла в нём.

И наоборот – косинус одного острого угла в прямоугольном треугольнике равен синусу другого острого угла в нём. Вот вам и подтверждение этого с помощью формул приведения:

Конечно, определить значения углов можно и без формул приведения, по тригонометрической окружности. И если вы умеете это делать, то очень хорошо. Но поняв, как работают формулы приведения, вы сможете делать это очень быстро.

Данные формулы можно также выразить в табличной форме:

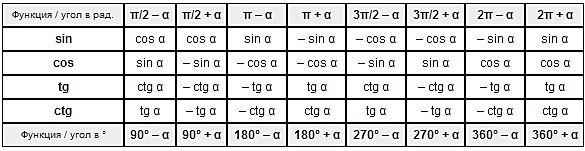
В дальнейшем, применяя свойство периодичности, четности (нечётности) вы без труда определите значение любого угла: 1050 0 , -750 0 , 2370 0 и любые другие. Статья об этом в будущем обязательно будет, не пропустите!

Когда в решениях задач буду использовать формулы приведения, то обязательно буду ссылаться на эту статью, чтобы вы всегда смогли освежить в памяти представленную выше теорию. На этом всё. Надеюсь, материал был вам полезен.

Формулы приведения — это соотношения, которые позволяют перейти от тригонометрических функций синус, косинус, тангенс и котангенс с углами `\frac <\pi>2 \pm \alpha`, `\pi \pm \alpha`, `\frac <3\pi>2 \pm \alpha`, `2\pi \pm \alpha` к этим же функциям угла `\alpha`, который находится в первой четверти единичной окружности. Таким образом, формулы приведения «приводят» нас к работе с углами в пределе от 0 до 90 градусов, что очень удобно.

Формулы приведения: список и таблицы

Всех вместе формул приведения есть 32 штуки. Они несомненно пригодятся на ЕГЭ, экзаменах, зачетах. Но сразу предупредим, что заучивать наизусть их нет необходимости! Нужно потратить немного времени и понять алгоритм их применения, тогда для вас не составит труда в нужный момент вывести необходимое равенство.

Сначала запишем все формулы приведения:

Для угла (`\frac <\pi>2 \pm \alpha`) или (`90^\circ \pm \alpha`):

`sin(\frac <\pi>2 — \alpha)=cos \ \alpha;` ` sin(\frac <\pi>2 + \alpha)=cos \ \alpha`
`cos(\frac <\pi>2 — \alpha)=sin \ \alpha;` ` cos(\frac <\pi>2 + \alpha)=-sin \ \alpha`
`tg(\frac <\pi>2 — \alpha)=ctg \ \alpha;` ` tg(\frac <\pi>2 + \alpha)=-ctg \ \alpha`
`ctg(\frac <\pi>2 — \alpha)=tg \ \alpha;` ` ctg(\frac <\pi>2 + \alpha)=-tg \ \alpha`

Для угла (`\pi \pm \alpha`) или (`180^\circ \pm \alpha`):

`sin(\pi — \alpha)=sin \ \alpha;` ` sin(\pi + \alpha)=-sin \ \alpha`
`cos(\pi — \alpha)=-cos \ \alpha;` ` cos(\pi + \alpha)=-cos \ \alpha`
`tg(\pi — \alpha)=-tg \ \alpha;` ` tg(\pi + \alpha)=tg \ \alpha`
`ctg(\pi — \alpha)=-ctg \ \alpha;` ` ctg(\pi + \alpha)=ctg \ \alpha`

Для угла (`\frac <3\pi>2 \pm \alpha`) или (`270^\circ \pm \alpha`):

`sin(\frac <3\pi>2 — \alpha)=-cos \ \alpha;` ` sin(\frac <3\pi>2 + \alpha)=-cos \ \alpha`
`cos(\frac <3\pi>2 — \alpha)=-sin \ \alpha;` ` cos(\frac <3\pi>2 + \alpha)=sin \ \alpha`
`tg(\frac <3\pi>2 — \alpha)=ctg \ \alpha;` ` tg(\frac <3\pi>2 + \alpha)=-ctg \ \alpha`
`ctg(\frac <3\pi>2 — \alpha)=tg \ \alpha;` ` ctg(\frac <3\pi>2 + \alpha)=-tg \ \alpha`

Для угла (`2\pi \pm \alpha`) или (`360^\circ \pm \alpha`):

`sin(2\pi — \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi — \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi — \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi — \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`

Часто можно встретить формулы приведения в виде таблицы, где углы записаны в радианах:

Чтобы воспользоваться ею, нужно выбрать строку с нужной нам функцией, и столбец с нужным аргументом. Например, чтобы узнать с помощью таблицы, чему будет равно ` sin(\pi + \alpha)`, достаточно найти ответ на пересечении строки ` sin \beta` и столбца ` \pi + \alpha`. Получим ` sin(\pi + \alpha)=-sin \ \alpha`.

И вторая, аналогичная таблица, где углы записаны в градусах:

Мнемоническое правило формул приведения или как их запомнить

Как мы уже упоминали, заучивать все вышеприведенные соотношения не нужно. Если вы внимательно на них посмотрели, то наверняка заметили некоторые закономерности. Они позволяют нам сформулировать мнемоническое правило (мнемоника — запоминать), с помощью которого легко можно получить любую с формул приведения.

Сразу отметим, что для применения этого правила нужно хорошо уметь определять (или запомнить) знаки тригонометрических функций в разных четвертях единичной окружности.Само привило содержит 3 этапа:

1. Аргумент функции должен быть представлен в виде `\frac <\pi>2 \pm \alpha`, `\pi \pm \alpha`, `\frac <3\pi>2 \pm \alpha`, `2\pi \pm \alpha`, причем `\alpha` — обязательно острый угол (от 0 до 90 градусов).
2. Для аргументов `\frac <\pi>2 \pm \alpha`, `\frac <3\pi>2 \pm \alpha` тригонометрическая функция преобразуемого выражения меняется на кофункцию, то есть противоположную (синус на косинус, тангенс на котангенс и наоборот). Для аргументов `\pi \pm \alpha`, `2\pi \pm \alpha` функция не меняется.
3. Определяется знак исходной функции. Полученная функция в правой части будет иметь такой же знак.

Чтобы посмотреть, как на практике можно применить это правило, преобразим несколько выражений:

1. ` cos(\pi + \alpha)`.

Функция на противоположную не меняется. Угол ` \pi + \alpha` находится в III четверти, косинус в этой четверти имеет знак «-» , поэтому преобразованная функция будет также со знаком «-» .

Ответ: ` cos(\pi + \alpha)= — cos \alpha`

2. `sin(\frac <3\pi>2 — \alpha)`.

Согласно мнемоническому правилу функция изменится на противоположную. Угол `\frac <3\pi>2 — \alpha` находится в III четверти, синус здесь имеет знак «-» , поэтому результат также будет со знаком «-» .

Ответ: `sin(\frac <3\pi>2 — \alpha)= — cos \alpha`

3. `cos(\frac <7\pi>2 — \alpha)`.

`cos(\frac <7\pi>2 — \alpha)=cos(\frac <6\pi>2+\frac <\pi>2-\alpha)=cos (3\pi+(\frac<\pi>2-\alpha))`. Представим `3\pi` как `2\pi+\pi`. `2\pi` — период функции.

Важно: Функции `cos \alpha` и `sin \alpha` имеют период `2\pi` или `360^\circ`, их значения не изменятся, если на эти величины увеличить или уменьшить аргумент.

Исходя из этого, наше выражение можно записать следующим образом: `cos (\pi+(\frac<\pi>2-\alpha)`. Применив два раза мнемоническое правило, получим: `cos (\pi+(\frac<\pi>2-\alpha)= — cos (\frac<\pi>2-\alpha)= — sin \alpha`.

Ответ: `cos(\frac <7\pi>2 — \alpha)=- sin \alpha`.

Лошадиное правило

Второй пункт вышеописанного мнемонического правила еще называют лошадиным правилом формул приведения. Интересно, почему лошадиным?

Итак, мы имеем функции с аргументами `\frac <\pi>2 \pm \alpha`, `\pi \pm \alpha`, `\frac <3\pi>2 \pm \alpha`, `2\pi \pm \alpha`, точки `\frac <\pi>2`, `\pi`, `\frac <3\pi>2`, `2\pi` — ключевые, они располагаются на осях координат. `\pi` и `2\pi` на горизонтальной оси абсцисс, а `\frac <\pi>2` и `\frac <3\pi>2` на вертикальной оси ординат.

Задаем себе вопрос: «Меняется ли функция на кофункцию?». Чтобы ответить на этот вопрос, нужно подвигать головой вдоль оси, на которой расположена ключевая точка.

То есть для аргументов с ключевыми точками, расположенными на горизонтальной оси, мы отвечаем «нет», мотая головой в стороны. А для углов с ключевыми точками, расположенными на вертикальной оси, мы отвечаем «да», кивая головой сверху вниз, как лошадь 🙂

Рекомендуем посмотреть видеоурок, в котором автор подробно объясняет, как запомнить формулы приведения без заучивания их наизусть.

Практические примеры использования формул приведения

Применение формул приведения начинается еще в 9, 10 классе. Немало задач с их использованием вынесено на ЕГЭ. Вот некоторые из задач, где придется применять эти формулы:

задачи на решение прямоугольного треугольника;
преобразования числовых и буквенных тригонометрических выражений, вычисление их значений;
стереометрические задачи.

Пример 1. Вычислите при помощи формул приведения а) `sin 600^\circ`, б) `tg 480^\circ`, в) `cos 330^\circ`, г) `sin 240^\circ`.

Решение: а) `sin 600^\circ=sin (2 \cdot 270^\circ+60^\circ)=-cos 60^\circ=-\frac 1 2`;

б) `tg 480^\circ=tg (2 \cdot 270^\circ-60^\circ)=ctg 60^\circ=\frac<\sqrt 3>3`;

в) `cos 330^\circ=cos (360^\circ-30^\circ)=cos 30^\circ=\frac<\sqrt 3>2`;

г) `sin 240^\circ=sin (270^\circ-30^\circ)=-cos 30^\circ=-\frac<\sqrt 3>2`.

Пример 2. Выразив косинус через синус по формулам приведения, сравнить числа: 1) `sin \frac <9\pi>8` и `cos \frac <9\pi>8`; 2) `sin \frac <\pi>8` и `cos \frac <3\pi>10`.

Решение: 1)`sin \frac <9\pi>8=sin (\pi+\frac <\pi>8)=-sin \frac <\pi>8`

`cos \frac <9\pi>8=cos (\pi+\frac <\pi>8)=-cos \frac <\pi>8=-sin \frac <3\pi>8`

`-sin \frac <\pi>8> -sin \frac <3\pi>8`

2) `cos \frac <3\pi>10=cos (\frac <\pi>2-\frac <\pi>5)=sin \frac <\pi>5`

`sin \frac <\pi>8 Доказательство формул приведения

Докажем сначала две формулы для синуса и косинуса аргумента `\frac <\pi>2 + \alpha`: ` sin(\frac <\pi>2 + \alpha)=cos \ \alpha` и` cos(\frac <\pi>2 + \alpha)=-sin \ \alpha`. Остальные выводятся из них.

Возьмем единичную окружность и на ней точку А с координатами (1,0). Пусть после поворота на угол `\alpha` она перейдет в точку `А_1(х, у)`, а после поворота на угол `\frac <\pi>2 + \alpha` в точку `А_2(-у,х)`. Опустив перпендикуляры с этих точек на прямую ОХ, увидим, что треугольники `OA_1H_1` и `OA_2H_2` равны, поскольку равны их гипотенузы и прилежащие углы. Тогда исходя из определений синуса и косинуса можно записать `sin \alpha=у`, `cos \alpha=х`, ` sin(\frac <\pi>2 + \alpha)=x`, ` cos(\frac <\pi>2 + \alpha)=-y`. Откуда можно записать, что ` sin(\frac <\pi>2 + \alpha)=cos \alpha` и ` cos(\frac <\pi>2 + \alpha)=-sin \alpha`, что доказывает формулы приведения для синуса и косинуса угла `\frac <\pi>2 + \alpha`.

Выходя из определения тангенса и котангенса, получим ` tg(\frac <\pi>2 + \alpha)=\frac 2 + \alpha)>2 + \alpha)>=\frac <-sin \alpha>=-ctg \alpha` и ` сtg(\frac <\pi>2 + \alpha)=\frac 2 + \alpha)>2 + \alpha)>=\frac <-sin \alpha>=-tg \alpha`, что доказывает формулы приведения для тангенса и котангенса угла `\frac <\pi>2 + \alpha`.

Чтобы доказать формулы с аргументом `\frac <\pi>2 — \alpha`, достаточно представить его, как `\frac <\pi>2 + (-\alpha)` и проделать тот же путь, что и выше. Например, `cos(\frac <\pi>2 — \alpha)=cos(\frac <\pi>2 + (-\alpha))=-sin(-\alpha)=sin(\alpha)`.

Углы `\pi + \alpha` и `\pi — \alpha` можно представить, как `\frac <\pi>2 +(\frac <\pi>2+\alpha)` и `\frac <\pi>2 +(\frac <\pi>2-\alpha)` соответственно.

А `\frac <3\pi>2 + \alpha` и `\frac <3\pi>2 — \alpha` как `\pi +(\frac <\pi>2+\alpha)` и `\pi +(\frac <\pi>2-\alpha)`.

Тригонометрия.Формулы приведения.

Формулы приведения не нужно учить их нужно понять. Понять алгоритм их вывода. Это очень легко!

Возьмем единичную окружность и расставим все градусные меры (0°; 90°; 180°; 270°; 360°) на ней.

Разберем в каждой четверти функции sin(a) и cos(a).

Запомним, что функцию sin(a) смотрим по оси Y, а функцию cos(a) по оси X.

В первой четверти видно, что функция sin(a)>0, потому что ось Y положительна в этой четверти.
И функция cos(a)>0, потому что ось X положительна в этой четверти.
Первую четверть можно описать через градусную меру, как (90-α) или (360+α).

Во второй четверти видно, что функция sin(a)>0, потому что ось Y положительна в этой четверти.
А функция cos(a) 0, потому что ось X положительна в этой четверти.
Четвертую четверть можно описать через градусную меру, как (270+α) или (360-α).

Теперь рассмотрим сами формулы приведения.

Запомним простой алгоритм:
1. Четверть. (Всегда смотрите в какой вы четверти находитесь).
2. Знак. (Относительно четверти смотрите положительны или отрицательный функции косинуса или синуса).
3. Если у вас есть в скобочках (90° или π/2) и (270° или 3π/2), то функция меняется.

И так начнем разбирать по четвертям данный алгоритм.

Выясни чему будет равно выражение cos(90-α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции косинуса положительный.
3. В скобочках есть (90° или π/2), то функция меняется с косинуса на синус.
Будет cos(90-α) = sin(α)

Выясни чему будет равно выражение sin(90-α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции синуса положительный.
3. В скобочках есть (90° или π/2), то функция меняется с синуса на косинус.
Будет sin(90-α) = cos(α)

Выясни чему будет равно выражение cos(360+α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции косинуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет cos(360+α) = cos(α)

Выясни чему будет равно выражение sin(360+α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции синуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(360+α) = sin(α)

Выясни чему будет равно выражение cos(90+α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции косинуса отрицательный.
3. В скобочках есть (90° или π/2), то функция меняется с косинуса на синус.
Будет cos(90+α) = -sin(α)

Выясни чему будет равно выражение sin(90+α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции синуса положительный.
3. В скобочках есть (90° или π/2), то функция меняется с синуса на косинус.
Будет sin(90+α) = cos(α)

Выясни чему будет равно выражение cos(180-α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции косинуса отрицательный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет cos(180-α) = cos(α)

Выясни чему будет равно выражение sin(180-α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции синуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(180-α) = sin(α)

Рассуждаю про третью и четвертую четверть подобным образом составим таблицу:

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

В тригонометрии, вообще, очень много разных формул. Их количество ни в коем случае не должно пугать школьника. Для того, чтобы успешно сдать ЕГЭ нужно не зубрить наизусть основные тригонометрические тождества, а понять их суть. Для многих формул разработаны даже специальные мнемонические правила, чтобы их можно было проще запомнить.

Один из самых сложных и запутанных, на взгляд ученика средней школы, раздел тригонометрических выражений – это формулы приведения. Для чего же они нужны? Отбросив вступление, скажем сразу – формулы приведения позволяют заменить функцию на кофункцию. Например, если в задании стоит синус α, его можно заменить на косинус α, и наоборот.

Функция	Кофункция
sin α	cos α
cos α	sin α
tg α	ctg α
ctg α	tg α

Формулы приведения

Так в каких же случаях необходимо применять формул приведения?! Все очень просто, с их помощью, можно заменить не только функцию, но и аргумент. Например, косинус тупого угла можно заменить на косинус или синус острого угла.

А теперь, внимательно рассмотрим список. Нетрудно заметить, что в нем присутствуют некие закономерности. Итак, для каждой функции существует 8 формул приведения: 2 с аргументами (π±α), 2 для угла (2π±α), по две на (π/2±α) и (3π/2±α). Если проанализировать перечень, то можно убедиться, что для первых 4-х аргументов смена функции на кофункцию не происходит. Попробуем переписать аргументы выражений не в радианах, а в градусах:

Загадка решена – каждая пара формул описывает поведение функции в той или иной четверти тригонометрической окружности.

Осталось вывести мнемонические правила для формул приведения и запомнить их.

Мнемонические правила формул приведения

Мнемоника – это совокупность правил, приемов и подсказок, облегчающих запоминание информации, путем создания устойчивых ассоциаций. Для подобных «правил» используют яркие и необычные образы. Всем известны «пифагоровы штаны» и стишок глаголов на спряжение:

Оба примера являются яркой иллюстрацией мнемонических правил.

Чтобы быстро и безошибочно восстановить любую формулу приведения необходимо выполнить три пункта:

Представить исходный аргумент в требуемом виде: (π±α), (2π±α), (π/2±α) или (3π/2±α).
Определить какой знак имеет исходная функция в требуемой четверти.
Заменить при необходимости функцию на кофункцию: в случаях (π±α) и (2π±α) функция не меняется,а при (π/2±α) или (3π/2±α) происходит смена тригонометрического выражения при аргументе.

Разберем конкретный пример подобных преобразований.

Задача 1.

Привести tg 750° к тригонометрическим функциям острого угла. Решение: Аргумент тангенса можно записать разными способами.

tg 750° = tg (2*360° + 30°) = tg (2π + 30°+2π);
tg 750° = tg (90° – 60° + 2*360°)= tg (π/2-60° +4π).

Лишними 2π и 4π в обоих случаях можно пренебречь, так как каких-либо серьезных изменений они не вносят. Если поставить карандаш в точку пересечения луча, выходящего из центра окружности под углом к оси ОХ в 𝜋2−60° или (2𝜋+30°), и дуги окружности, а затем совершить 1 или 2 оборота в 360°, карандаш все равно вернется в исходную точку.

Оба угла 30° и 60° расположены в первой четверти круга, где знак для тангенса – «+». Следовательно, и знак перед новыми функциями будет положительным. Для угла (2π + 30°) функция останется неизменной, а для (π/2-60°) – сменится на кофункцию:

tg 750° = tg (2π + 30° )=tg 30°
tg 750° = tg (π/2-60°)=ctg 60°

Обратимся к тождествам и проверим результат.

Лошадиное правило

Такое необычное название получил один способ, как запомнить смену функции на кофунцию. По легенде в давние времена жил на свете очень рассеянный математик. И был у него один верный и умный друг – лошадь. Занимаясь тригонометрией математик спрашивал лошадь менять ему функцию или нет, если животное кивало головой происходила замена, нет – все оставалось «на месте».

Разобраться в истории довольно просто, если представить ось координат для построения тригонометрической окружности. Если аргумент функции содержит
, то есть лошадь кивает «да», происходит смена на кофункцию. Если же перед острым углом стоит π или 2π, умный конь кивает вдоль оси OX – «нет», функция остается прежней.

Единственное что необходимо заучить наизусть – это знаки по четвертям для sin, cos, tg и ctg. Существует таблица перехода знаков, но для легкого запоминания она бесполезна.

Тригонометрический круг со знаками для каждой функции гораздо удобнее.

Правило ладони

Еще одно очень удобное мнемоническое правило, разработано для запоминания значений арксинусов и арккосинусов острых углов. Благодаря этому методу для расчета «арков» на ЕГЭ школьнику понадобится только собственная ладонь.

Если представить, что через большой палец и мизинец проходят оси координат OY и OX, тогда пальцы представляют собой лучи под углами 0, 30°, 45°, 60° и 90°.

Запомним простую формулу

Теперь, чтобы узнать значение arcsin α необходимо подставить вместо n «номер пальца»: 0, 1, 2, 3 или 4. Для arcos α нумеровать необходимо в обратном порядке от 4 до 0.

10 класс. Алгебра.

Формулы приведения относятся к тригонометрической функции, которая использует периодичность для преобразования тригонометрической функции с относительно большим углом в тригонометрическую функцию с относительно небольшим углом.

Формулы взаимосвязи между углами противоположными на 360 градусов или круг

Эти формулы устанавливают связь между углами противоположными на 360 градусов или круг. Значение одной и той же тригонометрической функции для того же угла на противоположной стороне равно.

Пусть α — любой острый угол, выражение угла в радианной системе:

$cos(2k \pi+\alpha)=cos \alpha$
$(k \in Z)$

$sin(2k \pi+\alpha)=sin \alpha$
$(k \in Z)$

$tg(2k \pi+\alpha)=tg \alpha$
$(k \in Z)$

$ctg(2k \pi+\alpha)=ctg \alpha$
$(k \in Z)$

В градусной мере тригонометрическая функция угла будет выражаться формулами:

$sin(\alpha+k \cdot 360^0)=sin \alpha$
$(k \in Z)$
.
$cos(\alpha+k \cdot 360^0)=cos \alpha$
$(k \in Z)$
.
$tg(\alpha+k \cdot 360^0)=tg \alpha$
$(k \in Z)$
.
$ctg(\alpha+k \cdot 360^0)=ctg \alpha$
$(k \in Z)$
.
$sec(\alpha+k \cdot 360^0)=sec \alpha$
$(k \in Z)$
.
$cosec(\alpha+k \cdot 360^0)=cosec \alpha$
$(k \in Z)$
.

Формулы тригонометрической функции π + α, связанные с значением тригонометрической функции α

Эта группа устанавливает связь между значением тригонометрической функции π + α и значением тригонометрической функции α.

Пусть α — любой угол, выражение угла в радианной системе:

sin (π+α)=－sinα.
cos (π+α)=－cosα.
tg (π+α)=tgα.
ctg (π+α)=ctgα.
sec (π+α)=－secα.
cosec (π+α)=－cosecα.

В градусной мере:

sin (180°+α)=－sinα.
cos (180°+α)=－cosα.
tg (180°+α)=tgα.
ctg (180°+α)=ctgα.
sec (180°+α)=－secα.
cosec (180°+α)=－cosecα.

Связь между значением тригонометрической функции любого угла α и -α

Приведем формулы приведения, в которых устанавливается связь между значением тригонометрической функции любого угла α и угла -α:

sin (-α) = — sinα.
cos (-α) = cosα.
tg (-α) = — tgα.
ctg (-α)=ctgα.
sec (-α) = secα.
cosec (-α) = — cosecα.

Связь между значениями тригонометрических функций π-α и α

Эти формулы могут быть получены по формулам связи между значениями тригонометрических функций углов α и -α и между значением тригонометрической функции π + α и значением тригонометрической функции α :

Представление угла в радианной мере:
sin (π － α) = sinα.
cos (π － α) = — cosα.
tg (π － α) = — tgα.
ctg (π － α) = — ctgα.
sec (π － α) = — secα.
cosec (π － α) = cosecα.

Представление угла в градусной мере:
sin (180 ° －α) = sinα.
cos (180 ° －α) = — cosα.
tg (180 ° －α) = — tgα.
ctg (180 ° －α) = — ctgα.
sec（180 ° －α) = — secα.
cosec (180 ° －α) = cosecα.

Связь между значением тригонометрической функции 2π-α и α

Эти формулы могут быть получены по формулам связи тригонометрических функций аргументов противоположных на круг и угла α и угла -α :

Представление угла в радианной мере:
sin (2π － α) = — sinα.
cos (2π － α) = cosα.
tg (2π － α) = — tgα.
ctg (2π － α) = — ctgα.
sec (2π － α) = secα.
cosec (2π － α) = — cosecα.

Представление в градусной мере:
sin (360 ° －α) = — sinα.
cos （360 ° －α） = cosα.
tg (360 ° －α) = -tgα.
ctg (360 ° －α) = — ctgα.
sec（360 ° －α） = secα.
cosec (360 ° －α) = — cosecα.

Связь между значениями тригонометрических функций π/2 ± α и 3π/2 ± α и α

Связь между π / 2 + α и значением тригонометрической функции α

Представление угла в радианной мере:

sin (π / 2 + α) = cosα.
cos (π / 2 + α) = — sinα.
tg (π / 2 + α) = — ctgα.
ctg (π / 2 + α) = — tgα.
sec (π / 2 + α) = — cosecα.
cosec (π / 2 + α) = secα.

Представление угла в градусах:

sin (90 ° + α) = cosα.
cos (90 ° + α) = — sinα.
tg (90 ° + α) = -ctgα.
ctg (90 ° + α) = -tgα.
sec (90 ° + α) = -cosecα.
cosec (90 ° + α) = secα.

Связь между π / 2-α и значением тригонометрической функции α

Представление угла в радианной системе:

sin (π / 2 － α) = cosα.
cos (π / 2 － α) = sinα.
tg (π / 2 － α) = ctgα.
ctg (π / 2 － α) =tgα.
sec (π / 2 － α) = cosecα.
cosec (π / 2 － α) = secα.

Представление угла в градусах:

sin (90 ° －α) = cosα.
cos (90 ° －α) = sinα.
tg (90 ° －α) = ctgα.
ctg (90 ° －α) = tgα.
sec (90 ° －α) = cosecα.
cosec (90 ° －α) = secα.

Связь между 3π / 2 + α и значением тригонометрической функции α

Представление угла в радианах:

sin (3π / 2 + α) = — cosα.
cos (3π / 2 + α) = sinα.
tg (3π / 2 + α) = — ctgα.
ctg (3π / 2 + α) = -tgα.
sec (3π / 2 + α) = cosecα.
cosec (3π / 2 + α) = — secα.

Представление угла в градусах:

sin (270 ° + α) = — cosα.
cos (270 ° + α) = sinα.
tg (270 ° + α) = -ctgα.
ctg（270 ° + α） = -tgα.
sec (270 ° + α) = cosecα.
cosec (270 ° + α) = — secα.

Связь между 3π / 2 － α и значением тригонометрической функции α

Представление угла в радианах:

sin (3π / 2- α) = — cosα.
cos (3π / 2 -α) = — sinα.
tg (3π / 2 － α) =ctgα.
ctg (3π / 2 — α) =tgα.
sec (3π / 2 － α) = -cosecα.
cosec (3π / 2 － α) = — secα.

Представление угла в градусах:

sin (270 ° －α) = — cosα.
cos (270 ° －α) = — sinα.
tg（270 ° －α） = tgα.
ctg（270 ° －α） =tgα.
sec (270 ° －α) = -cosecα.
cosec (270 ° －α) = — secα.

Правило определения приведенной функции

Приведенные выше формулы приведения можно резюмировать так: для значения тригонометрической функции kπ / 2 ± α (k∈Z),

Когда k — четное число, значение приведенной функции будет с тем же именем, что и приводимая функция, но для α (острый угол), то есть имя функции не изменяется
Когда k — нечетное число, мы возьмем ко-функцию, но уже для α (острый угол), а именно sin (kπ / 2 ± α) → cosα; cos (kπ / 2 ± α) → sinα; tg (kπ / 2 ± α) → ctgα, ctg (kπ / 2 ± α) → tgα.

То есть мы получим:

$\ sin(2\pi k+\alpha)=\sin \alpha$
(1)

$\cos(2 \pi k + \alpha)=\cos \alpha$
(2)

Правило лошади в тригонометрии

Математики придумывают все новые и новые способы заставить ученика выучить это несложное правило, что придумали даже «кивающую лошадь». А правило, которое с ее помощью легче запомнить — это как раз вторая часть правила, когда k — нечетное число. В этом случае угол отсчитывается по вертикали. И тогда воображаемая лошадь кивает головой и функция меняется на ко-функцию. На наш взгляд абсолютно лишняя информация. Но если вам удобно — пользуйтесь.

Правило лошади в тригонометрии

Например:
sin (2π-α) = sin (4 · π/2-α), k = 4 — четное число, поэтому берется та же функция sinα.
Когда α — острый угол, 2π-α∈ (270°, 360°), sin (2π-α) Знаки тригонометрических функций

Формулы приведения в тригонометрии таблица

Все формулы приведения тригонометрических функций можно собрать в одну таблицу.

Формулы и правило приведения тригонометрических функций часто используются при решении тригонометрических уравнений и неравенств.

Примеры применения формул приведения

Пример 1

Вычислите $\sin 930^<\circ>$
.

Решение: Выделим целое количество тригонометрических кругов, каждый из которых $360^<\circ>$
. Получим: $\sin 930^<\circ>= \sin <(2 \cdot 360^<\circ>+210^<\circ>)>$
По формуле приведения из таблицы находим: $\sin<(2 \cdot 360^<\circ>+210^<\circ>)>=-\sin 210^<\circ>$

$\sin 210^<\circ>=\sin<(180^<\circ>+30^<\circ>)>=-\sin30^<\circ>$
, подставляем $\sin<(2 \cdot 360^<\circ>+210^<\circ>)>=-\sin 210^<\circ>=-(-\sin30^<\circ>)=\sin30^<\circ>=\frac<1><2>=0,5$
.

Пример 2

Вычислите $\cos 150^<\circ>$
.

Решение: Представим, $\cos 150^<\circ>=\cos<(90^<\circ>+60^<\circ>)>$
.

Для решения воспользуемся правилом, так как у нас получается нечетное число k и функция поменяется на ко-функцию, то есть был косинус, станет синус. Определимся со знаком, посмотрим, в какую четверть попадает $\cos<(90^<\circ>+60^<\circ>)>$
— это вторая четверть, косинус во второй четверти отрицательный, значит перед синусом поставим знак минус ( ставим знак приводимой функции, а приводим мы косинус ):

$\cos<(90^<\circ>+60^<\circ>)>=-\sin 60^<\circ>=-\frac<\sqrt<3>><2>$
.

Пример 3

Вычислите $\sin 135^<\circ>$
.

Решение: Проведем преобразования и применим правило приведения тригонометрических функций $\sin (90^<\circ>+45^<\circ>)=\cos 45^<\circ>=\frac<\sqrt<2>><2>$
.

Пример 4

Используя формулы приведения, вычислить:

$tg<\frac<5\pi><4>>$
.

Представим $\frac<5\pi><4>=\frac<4\pi+\pi><4>=\pi+\frac<\pi><4>$

Тогда, $tg<\frac<5\pi><4>>=tg<\pi+\frac<\pi><4>>=tg<\frac<\pi><4>>=1$

Ответ: $tg<\frac<5\pi><4>>=1$
.

Пример 5

$<\Hugo \frac<ctg(\frac<\pi><2>-\alpha)-tg (\pi+\alpha)+\sin (\frac<3\pi><2>-\alpha)><\cos(\pi+\alpha)>>$
.

Приведем тригонометрические функции согласно правилу приведения, получим:

$<\Hugo \frac<ctg(\frac<\pi><2>-\alpha)-tg (\pi+\alpha)+\sin (\frac<3\pi><2>-\alpha)><\cos(\pi+\alpha)>> = <\Hugo \frac<tg \alpha-tg \alpha-\cos \alpha><- \cos \alpha>>=\frac<-\cos \alpha><-\cos \alpha>=1$
.

Ответ:

Таким образом, чтобы правильно выполнить приведение тригонометрической функции большого угла к тригонометрической функции меньшего угла вы можете использовать формулы приведения, которые нужно будет выучить наизусть, а их свыше 50, можно облегчить себе запоминание — выучив таблицу. Или же воспользоваться простым правилом (рекомендуется). Удачи на экзаменах.

Читайте также: