Как построить график функции кос
Опубликовано: 17.09.2024
п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла
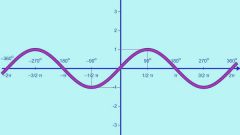
Рассмотрим, как изменяется косинус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=cosx на этом отрезке.

Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x косинусоидой .
Часть косинусоиды для –π≤x≤π называют волной косинусоиды .
Часть косинусоиды для \(-\frac\pi2\leq x\leq\frac\pi2\) называют полуволной или аркой косинусоиды .
Заметим, что термин «косинусоида» используется достаточно редко. Обычно, и в случае косинуса, говорят о «синусоиде».
п.2. Свойства функции y=cosx
1. Область определения \(x\in\mathbb
2. Функция ограничена сверху и снизу $$ -1\leq cosx\leq 1 $$ Область значений \(y\in[-1;1]\)
3. Функция чётная $$ cos(-x)=cosx $$
4. Функция периодическая с периодом 2π $$ cos(x+2\pi k)=cosx $$
5. Максимальные значения \(y_
6. Функция возрастает на отрезках $$ -\pi+2\pi k\leq x\leq 2\pi k $$ Функция убывает на отрезках $$ 2\pi k\leq x\leq\pi+2\pi k $$
7. Функция непрерывна.
п.3. Примеры
Пример 1. Найдите наименьшее и наибольшее значение функции y=cosx на отрезке:

a) \(\left[\frac\pi6; \frac<3\pi><4>\right]\) $$ y_
Пример 2. Решите уравнение графически:
a) \(cosx=\frac\pi2-x\)

Один корень: \(x=\frac\pi2\)
б) \(cosx-x=1\)
\(cosx=x+1\)

Один корень: x = 0
в) \(cosx-x^2=1\)
\(cosx=x^2+1\)

Один корень: x = 0
г*) \(cosx-x^2+\frac<\pi^2><4>=0\)
\(cosx=x^2-\frac<\pi^2><4>\)
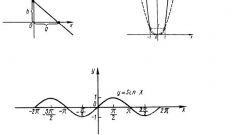
\(y=x^2-\frac<\pi^2><4>\) – парабола ветками вверх, с осью симметрии \(x_0=0\) (ось OY) и вершиной \(\left(0; -\frac<\pi^2><4>\right)\) (см. §29 справочника для 8 класса)

Два корня: \(x_<1,2>=\pm\frac\pi2\)
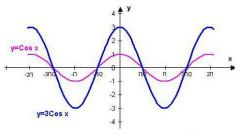
Пример 3. Постройте в одной системе координат графики функций $$ y=cosx,\ \ y=-cosx,\ \ y=2cosx,\ \ y=cosx-2 $$

\(y=-cosx\) – отражение исходной функции \(y=cosx\) относительно оси OX. Область значений \(y\in[-1;1]\).
\(y=2cosx\) – исходная функция растягивается в 2 раза по оси OY. Область значений \(y\in[-2;2]\).
\(y=cosx-2\) - исходная функция опускается вниз на 2. Область значений \(y\in[-3;-1]\).
Пример 4. Постройте в одной системе координат графики функций $$ y=cosx,\ \ y=cos2x,\ \ y=cos\frac

Амплитуда колебаний у всех трёх функций одинакова, область значений \(y\in[-1;1]\).
Множитель под косинусом изменяет период колебаний.
\(y=cosx\) – главная арка косинуса соответствует отрезку \(-\frac\pi2\leq x\leq\frac\pi2\)
\(y=cos2x\) - период уменьшается в 2 раза, главная арка укладывается в отрезок \(-\frac\pi4\leq x\leq\frac\pi4\).
\(y=cos\frac

- Как построить график cos
- Как построить синусоиду
- Как построить график по функции в Excel
- Как найти наименьший положительный период функции
- - лист бумаги (лучше в клетку);
- - линейка;
- - карандаш и ручка;
- - ластик;
- - калькулятор.
- Как вычислить функцию и построить график
- Как для графика составить уравнение
- Как по функции вычислить формулу
- Как построить график функций cos
![Как построить график функций cos]()
- Как построить график сдвигов и деформаций
![Как построить график сдвигов и деформаций]()
- Как строить график координат
![Как строить график координат]()
- Как построить график тригонометрической функции
![Как построить график тригонометрической функции]()
- Как построить график заданной функции
![Как построить график заданной функции]()
- Как построить график по точкам
![Как построить график по точкам]()
- Как начертить график функции
![Как начертить график функции]()
- Как начертить график
![Как начертить график]()
- Как строить графики функций
![Как строить графики функций]()
- Как найти наименьший период функции
![Как найти наименьший период функции]()
- Как построить график линейной функции
![Как построить график линейной функции]()
- Как построить график в Matlab
![Как построить график в Matlab]()
- Как исследовать функцию и построить ее график
![Как исследовать функцию и построить ее график]()
- Как решать графики функций
![Как решать графики функций]()
- Как нарисовать в ворде график
![Как нарисовать в ворде график]()
- Как построить в Word график функции
![Как построить в Word график функции]()
- Как построить график параболы
![Как построить график параболы]()
- Как по графику производной построить график функции
![Как по графику производной построить график функции]()
Урок и презентация на тему: "Функция y=cos(x). Определение и график функции"
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине "Интеграл" для 10 класса
Алгебраические задачи с параметрами, 9–11 классы
Что будем изучать:
1. Определение.
2. График функции.
3. Свойства функции Y=cos(X).
4. Примеры.
Определение функции косинуса у=cos(x)
Ребята, мы уже познакомились с функцией Y=sin(X).
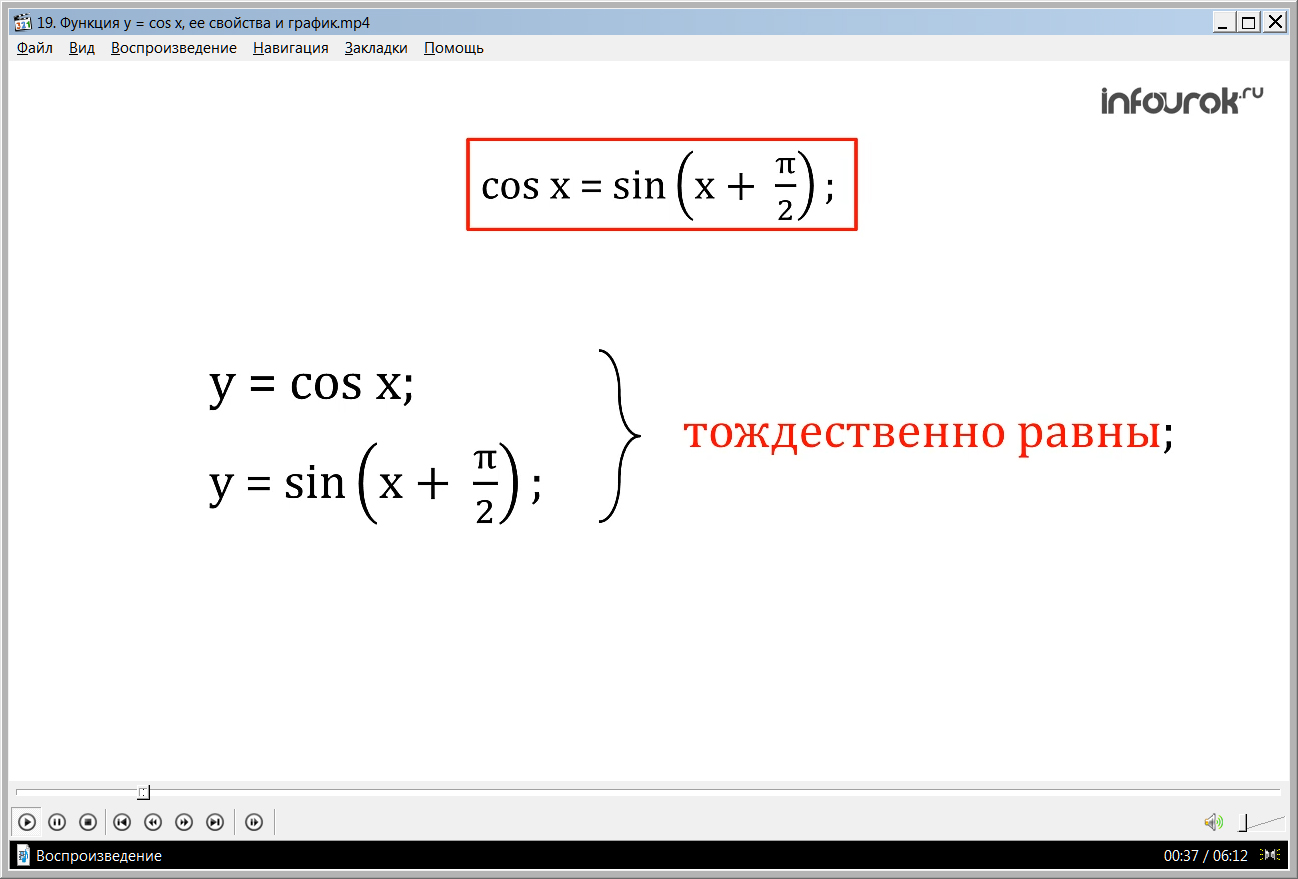
Давайте вспомним одну из формул привидения: sin(X + π/2) = cos(X).
Благодаря этой формуле, мы можем утверждать, что функции sin(X + π/2) и cos(X) тождественны, и их графики функций совпадают.
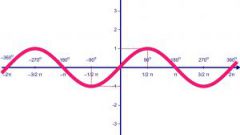
График функции sin(X + π/2) получается из графика функции sin(X) параллельным переносом на π/2 единиц влево. Это и будет график функции Y=cos(X).
_1.jpg)
График функции Y=cos(X) так же называют синусоидой.
Свойства функции cos(x)
-
Запишем свойства нашей функции:
- Область определения – множество действительных чисел.
- Функция четная. Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.
- Функция Y=cos(X) убывает на отрезке [0; π] и возрастает на отрезке [π; 2π]. В этом мы можем убедиться на графике нашей функции.
- Функция Y=cos(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ cos(X) ≤ 1 - Наименьшее значение функции равно -1 (при х = π + 2πk). Наибольшее значение функции равно 1 (при х = 2πk).
- Функция Y=cos(X) является непрерывной функцией. Посмотрим на график и убедимся, что у нашей функции нет разрывов, это и означает непрерывность.
- Область значений отрезок [- 1; 1]. Это также хорошо видно из графика.
- Функция Y=cos(X) - периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.
Примеры с функцией cos(x)
1. Решить уравнение cos(X)=(x - 2π) 2 + 1
Решение: Построим 2 графика функции: y=cos(x) и y=(x - 2π) 2 + 1 (см. рисунок). _2.jpg)
2 + 1" title="Графики функции y=cos(x) и y=(x - 2π) 2 + 1 " style="display: block; margin-left: auto; margin-right: auto;" />
y=(x - 2π) 2 + 1 - это парабола, смещенная вправо на 2π и вверх на 1. Наши графики пересекаются в одной точке А(2π;1), это и есть ответ: x = 2π.
2. Построить график функции Y=cos(X) при х ≤ 0 и Y=sin(X) при x ≥ 0
Решение: Чтобы построить требуемый график, давайте построим два графика функции по "кусочкам". Первый кусочек: y=cos(x) при х ≤ 0. Второй кусочек: y=sin(x)
при x ≥ 0. Изобразим оба "кусочка" на одном графике.
_3.jpg)
3. Найти наибольшее и наименьшее значение функции Y=cos(X) на отрезке [π; 7π/4]
Решение: Построим график функции и рассмотрим наш отрезок [π; 7π/4]. На графике видно, что наибольшие и наименьшие значения достигаются на концах отрезка: в точках π и 7π/4 соответственно.
Ответ: cos(π) = -1 – наименьшее значение, cos(7π/4) = наибольшее значение.
![Функция Y=cos(X) на отрезке [π; 7π/4]](https://mathematics-tests.com/images/stories/matematika/10-klass/10-klass-y=cos(x)_4.jpg)
4. Построить график функции y=cos(π/3 - x) + 1
Решение: cos(-x)= cos(x), тогда искомый график получится путем переноса графика функции y=cos(x) на π/3 единиц вправо и 1 единицу вверх.
_5.jpg)
Задачи для самостоятельного решения
1)Решить уравнение: cos(x)= x – π/2.
2) Решить уравнение: cos(x)= - (x – π) 2 - 1.
3) Построить график функции y=cos(π/4 + x) - 2.
4) Построить график функции y=cos(-2π/3 + x) + 1.
5) Найти наибольшее и наименьшее значение функции y=cos(x) на отрезке [0; 5π/3].
6) Найти наибольшее и наименьшее значение функции y=cos(x) на отрезке [- π/6; 5π/4].
Построим график функции . При этом нам опять пригодятся часы из разд. 2.1.
Если , то, очевидно, . Когда возрастает от 0 до , число возрастает от 0 до 1 (представьте себе, как меняется ордината конца стрелки на наших фирменных часах). Участок графика для от 0 до изображен на рис. 44. При
| \epsfbox |
малых наш график близок к прямой : вспомним, что при малых верна приближенная формула . Можно сказать, что прямая касается кривой с уравнением в точке . Заметим также, что наш участок графика расположен ниже этой прямой: ведь для острых углов , измеренных в радианах, выполнено неравенство (рис. 46а).
| \begin |
Задача 7.1 Запишите уравнение прямой, касающейся графика функции в точке с координатами .
Кривая на рис 45б центрально симметрична относительно точки с координатами ; это следует из другой формулы приведения: (рис. 46б).
После того, как у нас есть участок графика функции для , весь график строится уже просто. В самом деле, когда конец стрелки прошел путь , стрелка вернулась в исходное положение; при дальнейшем движении все будет повторяться. Значит, график будет состоять из таких же кусков, как на рис 45б. Окончательно график функции выглядит так, как на рис. 47.
| \epsfbox |
При этом участки графика при , , . получаются из графика на рис 45б сдвигом вдоль оси абсцисс на , , . соответственно. Это - просто переформулировка того факта, что функция имеет период .
Теперь построим график функции . Можно было бы строить его так же, как мы строили график синуса. Мы, однако, изберем другой путь, который позволит использовать уже имеющуюся у нас информацию.
Именно, воспользуемся формулой приведения . Эту формулу можно понимать так: функция принимает те же значения, что и функция , но на раньше. Например, функция принимает значение 1 при , а функция принимает это же значение уже при . На графике это означает следующее: для каждой точки графика есть точка графика , у которой ордината та же, а абсцисса на меньше (рис. 48).
| \epsfbox |
Стало быть, график получится, если сдвинуть график вдоль оси абсцисс на влево. На рис. 48 график функции изображен сплошной кривой.
Итак, мы выяснили, что график косинуса получается преобразованием (сдвигом) из графика синуса. Случаи, когда график одной функции можно получить преобразованием из графика другой функции, интересны и сами по себе, поэтому скажем о них несколько слов.
Как, например, будет выглядеть график функции ? Ясно, что ординаты точек этого графика получаются из ординат соответствующих точек графика умножением на 2, так что наш график изобразится сплошной кривой на рис. 49. Можно сказать, что график получается из графика растяжением в два раза вдоль оси ординат.
| \epsfbox |
| \epsfbox |
Теперь построим график функции . Легко понять, что функция принимает те же самые значения, что и функция , но при в два раза меньших значениях . Например, функция принимает значение 1 при , а функция - уже при ; иными словами, чтобы получить график , надо абсциссы всех точек графика уменьшить в два раза, а ординаты оставить неизменными. То, что получается, изображено на рис. 50. Можно сказать, что график (сплошная линия на рис. 50) получается из графика сжатием в 2 раза к оси ординат.
Попробуем еще построить график функции . Понятно, что он должен получаться каким-то преобразованием из графика . На первый взгляд может показаться, что это преобразование -- сдвиг влево на вдоль оси абсцисс, по аналогии с тем, что изображено на рис. 48. Однако, если бы это было так, то вышло бы, например, что функция принимает значение 1 при , что не соответствует действительности (проверьте!). Правильно рассуждать так: , так что функция принимает те же значения, что и функция , но на раньше. Так что сдвиг влево - не на , а на (рис. 51).
| \epsfbox |
Кривые, являющиеся графиками функций , где , , называются синусоидами. Заметим, что кривой ``косинусоида'' вводить не надо: как мы видели, график косинуса - это та же кривая, что и график синуса, только иначе расположенная относительно осей координат.
Задача 7.2 Каковы координаты точек, помеченных на рис. 51 вопросительными знаками?
Задача 7.3 Возьмите свечу, тонкий лист бумаги и острый нож. Намотайте лист бумаги на свечу в несколько слоев и аккуратно разрежьте эту свечу вместе с бумагой наискосок ножом. Теперь разверните бумагу. Вы увидите, что она оказалась разрезанной по волнистой линии. Докажите, что эта волнистая линия является синусоидой.
Задача 7.4 Постройте графики функций:
Замечание. Если вы строите графики тригонометрических функций на клетчатой бумаге, удобно выбрать немного разные масштабы по осям, с тем чтобы на оси абсцисс числу соответствовало целое число клеточек. Например, часто выбирают такой масштаб: по оси ординат отрезок длины 1 занимает две клеточки, по оси абсцисс отрезок длины занимает 6 клеточек.
Задача 7.5 Постройте графики функций: а) ; б) .
Посмотрим, как выглядят на графиках уже известные нам решения уравнений и . Эти решения являются абсциссами точек пересечения горизонтальной прямой с графиком функций (соответственно ). На рис. 52, 53 хорошо видны две серии решений, получающихся при
| \epsfbox |
| \epsfbox |
По графикам синуса и косинуса видно, на каких промежутках эти функции возрастают, а на каких убывают. Ясно, например, что функция возрастает на отрезках , , . - одним словом, на всех отрезках , где >$" width="53" height="37" />
, и убывает на всех отрезках , где >$" width="54" height="36" />
.
Задача 7.6 На каких отрезках возрастает и на каких убывает функция ?
Задача 7.7 Сравните числа:
$\cos7$; \\ [2pt] д) $\cos7$ и
Задача 7.8 Расположите в порядке возрастания: , , , , , .
БесплатноКраткое описание документа:
Видеоурок «Функция у = cos х, ее свойства и график» представляет наглядный материал для изучения данной темы. В пособии представлены особенности функции, ее свойства, а также описания решения задач, в которых применяются знания о свойства косинуса. С помощью видеоурока учителю легче предоставить требуемые знания и сформировать умения учеников. Наглядное пособие может помочь повысить эффективность урока, обеспечив более глубокое понимание материала и лучшее запоминание, а также освободив время урока для проведения индивидуальной работы.
Использование видеоурока дает учителю преимущество для более эффективной подачи материала. Пособие может применяться только для наглядности, сопровождая объяснение учителя или в качестве самостоятельной части урока, давая возможность учителю улучшить индивидуальную работу с учениками. Демонстрируемые построения графиков, преобразования в помощью анимационных эффектов становятся более понятными для учеников, помогают освоить навыки решения задач с использованием данного материала. Выделение и озвучивание свойств функции инструментами видеоурока помогает лучше их запомнить.
Демонстрация начинается с представления названия темы. Для построения графика функции у = cos х ученикам напоминается формула приведения cos х= sin (х+π/2), которая свидетельствует о том, что графики функций у= cos х и у= sin (х+π/2) являются тождественно равными. Для построения графика функции у= sin (х+π/2) стоится координатная плоскость, на оси абсцисс которой отмечается точка –π/2. Если взять эту точку за начало координат для построения графика sin х, то этот график является и графиком функции у= sin (х+π/2) для начала координат. То есть график функции у = cos х является на π/2 сдвинутым по оси абсцисс графика функции у= sin х. очевидно, что графиком функции у = cos х также является синусоида. Ее расположение позволяет сделать выводы о свойствах функции.
Первое свойство функции – об области определения. Очевидно, что областью определения функции будет вся числовая прямая, то есть D(f)=(- ∞;+∞).
Во втором свойстве функции отмечается четность функции. Ученикам напоминается изученный в 9 классе материал, в котором было указано условие четности функции. Для четной функции является справедливым равенство f(-x)=f(x). Говоря о четности функции косинуса, нужно отметить, что график этой функции симметричен относительно оси ординат. Продемонстрировать свойства функции можно на рисунке, где изображена на координатной плоскости единичная окружность. В первой и четвертой четвертях отмечены точки, симметричные относительно оси абсцисс. Косинус определяется абсциссой точки, поэтому для двух точек L(t) и N(-t) абсциссы одинаковые. Поэтому cos (-t)= cos t.
Третье свойство отмечает промежутки убывания и возрастания функции. В свойстве указано, что функция убывает на отрезке [0;π], а на отрезке [π;2π] косинус возрастает. На рисунке продемонстрирован график функции, на котором хорошо видно область убывания и возрастания функции.
Очевидно, что функция у = cos х возрастает на каждом отрезке [π+2πk;2π+2πk]. Отрезки убывания в общем виде выглядят так [2πk;π+2πk], где k – целое число.
В четвертом свойстве отмечается ограниченность функции косинуса сверху и снизу. Аналогично синусу, можно отметить ограниченность значений косинуса -1 2 . Решением данного уравнения будут точки пересечения графиков функций, которые представлены выражениями правой и левой части уравнения, то есть у = cos х и у=1-х 2 . Очевидно, что график первого уравнения – синусоида, продемонстрированная в теме ранее. График второй функции – парабола, вершина которой располагается в точке (0;1). Построив графики каждой функции, на рисунке к данной задаче видно, что единственной точкой пересечения двух графиков будет точка В(0;1).
Во втором примере необходимо построить и прочитать график функции, которая определяется на отрезке х =π/2 выражением cosx. На рисунке, сопровождающем решение примера, строится график функции у=sinx на отрезке [-3π/2; π/2]. При этом в точке π/2 функция не принимает значение. На отрезке [π/2; 3π/2] строится фрагмент функции у = cos х. Очевидно, построенные фрагменты будут повторяться по всей области определения. Далее описывается, как читается функция. Отмечается, что это означает описать ее свойства. Перечисляются свойства данной функции – область определения (-∞;+∞), отсутствие признаков четности или нечетности для всей области определения, ограниченность функции и сверху, и снизу. Наибольшим значением функции будет 1, а наименьшим -1. Также отмечается наличие разрыва в точке х=π/2, множество значений функции (-1;1).
Видеоурок «Функция у = cos х, ее свойства и график» применяется на уроке математики по данной теме в качестве наглядного материала. Также данное видео может быть полезным для формирования необходимых умений у учеников учителю, который проводит обучение дистанционно. Материал может быть рекомендован для самостоятельного рассмотрения ученикам, которые недостаточно хорошо освоили тему и требуют дополнительных занятий.
Прежде чем построить график функции у = cos x, вспомним формулу приведения, по которой cos x = sin( x + 14ПЂ2)"> (косинус аргумента икс равен синусу аргумента икс плюс пи на два). Это значит, что функции у = cos x и
у = sin( x + 14ПЂ2)"> тождественно равны, следовательно их графики совпадают.
Для построения графика функции у = sin( x + 14ПЂ2)"> нам понадобится вспомогательная система координат с началом в точке В( - 14ПЂ2"> ; 0) ( в точке бэ с координатами минус пи на два , ноль).Если в новой системе координат построить график функции у = sin x, то получим график функции
у = sin( x + 14ПЂ2)"> или же график функции у = cos x, так как их графики совпадают( смотри рис.1).
Поскольку график функции у = cos x получается из графика синуса с помощью параллельного переноса на расстояние 14ПЂ2"> в отрицательном направлении, то график этой функции также является синусоидой.
Изображение графика функции у = cos x дает наглядное представление о свойствах этой функции .
СВОЙСТВО 1. Область определения – множество всех действительных чисел или D (f) = ( - 14в€ћ"> ; + 14в€ћ"> ) ( дэ от эф равно промежутку от минус бесконечности до плюс бесконечности).
СВОЙСТВО 2. Функция у = cos x четная.
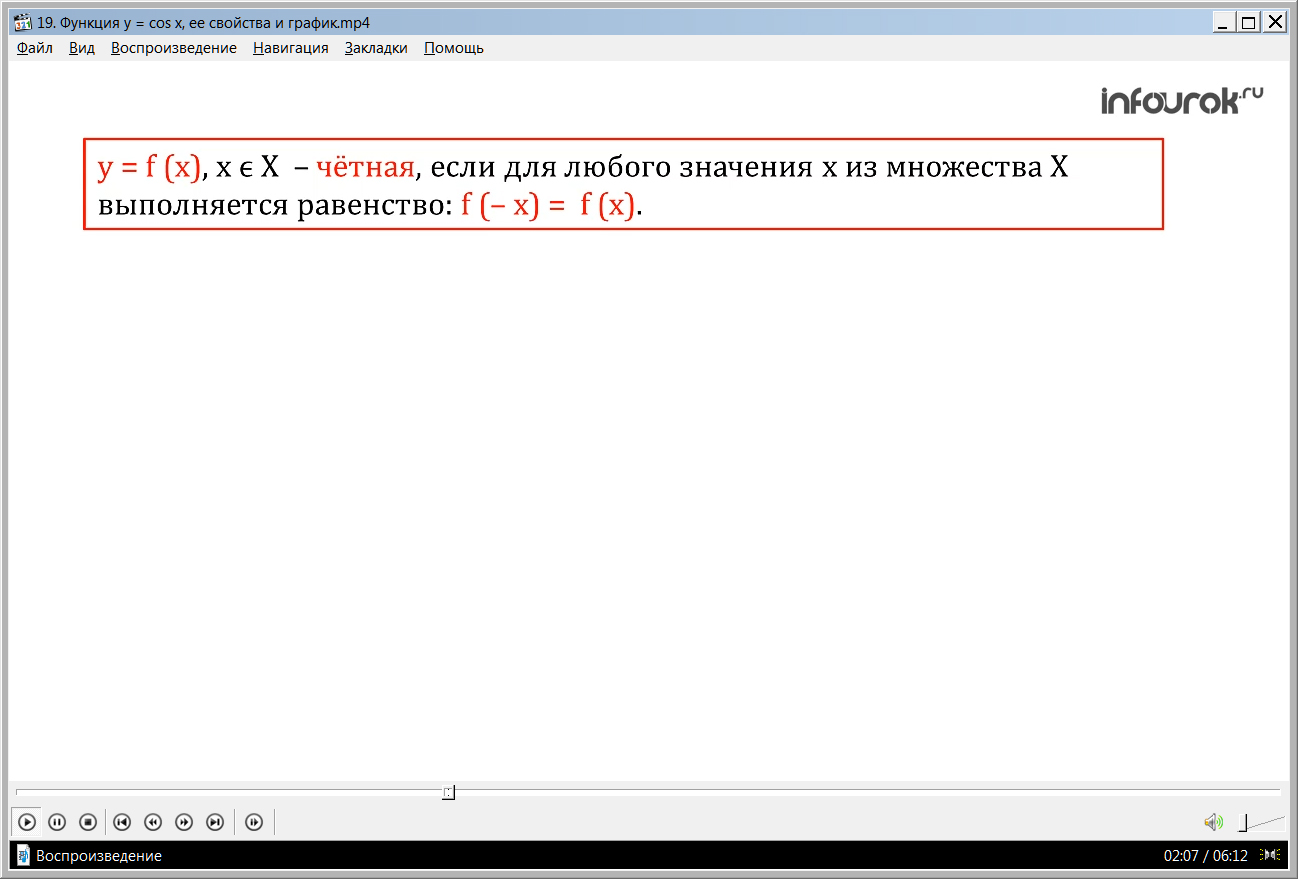
На уроках в 9 классе мы изучили, что функция у = f (x), х ϵХ ( игрек равно эф от икс, где икс принадлежит множеству икс большое) называется четной, если для любого значения х из множества Х выполняется равенство
f (- x) = f (x)( эф от минус икс равно эф от икс).
СВОЙСТВО 3.На отрезке [ 0 ; π ]( от нуля до пи) функция убывает, возрастает на отрезке [ π ; 2π ] ( от пи до двух пи) и так далее.
Можно сделать общий вывод: функция у = cos x возрастает на отрезке
[π 14+2ПЂk "> ; 142ПЂ+2ПЂk"> ] ( от пи плюс два пи ка до двух пи плюс два пи ка), а убывает на отрезке [ 14 2ПЂk"> ; 14ПЂ+2ПЂk]"> ( от двух пи ка до пи плюс два пи ка), где ( ка принадлежит множеству целых чисел).
СВОЙСТВО 4.Функция ограничена сверху и снизу.
СВОЙСТВО 5. Наименьшее значение функции равно минус единице и достигается в любой точке вида х = 14ПЂ+2ПЂk"> ( или можно записать унаим.= - 1); наибольшее значение равно 1 и достигается в любой точке вида х = 142ПЂk">
( или можно записать унаиб.= 1).
СВОЙСТВО 6.Функция у = cos x является непрерывной.
СВОЙСТВО 7. Множество значений функции – отрезок от минус одного до одного( или можно записать Е(f) = [ - 1; 1] ).
ПРИМЕР 1.Решить уравнение cos x= 1 – х 2 ( косинус икс равно один минус икс в квадрате).
Решение. Решим это уравнение графически. В одной системе координат построим два графика функций: у = cos x и у = 1 – х 2 . Графиком функции
у = 1 – х 2 является парабола, ветви которой направлены вниз, так как коэффициент при икс в квадрате отрицателен. ( см. рис.2) У построенных графиков только одна общая точка – это точка В( 0; 1)( бэ с координатами ноль, один).
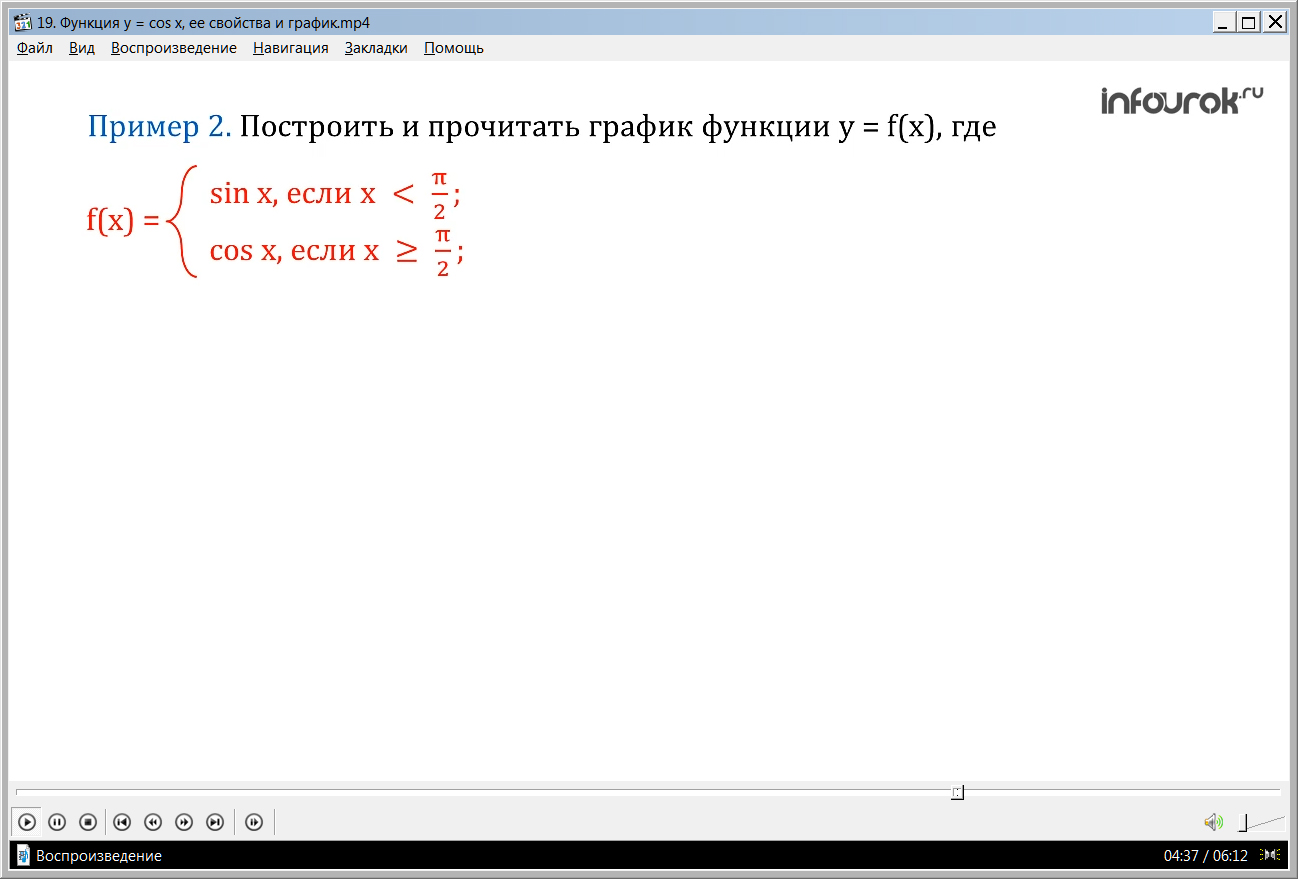
ПРИМЕР 2. Построить и прочитать график функции у = f( x), где
Решение. Строить график будем «по кусочкам». Сначала построим часть графика функции у = sin x на открытом луче ( - 14в€ћ"> ; 14ПЂ2"> ) , затем в этой же системе координат на луче [ 14 ПЂ2"> ; + 14в€ћ"> ) построим часть графика функции у = cos x. Получим график функции у = f( x).
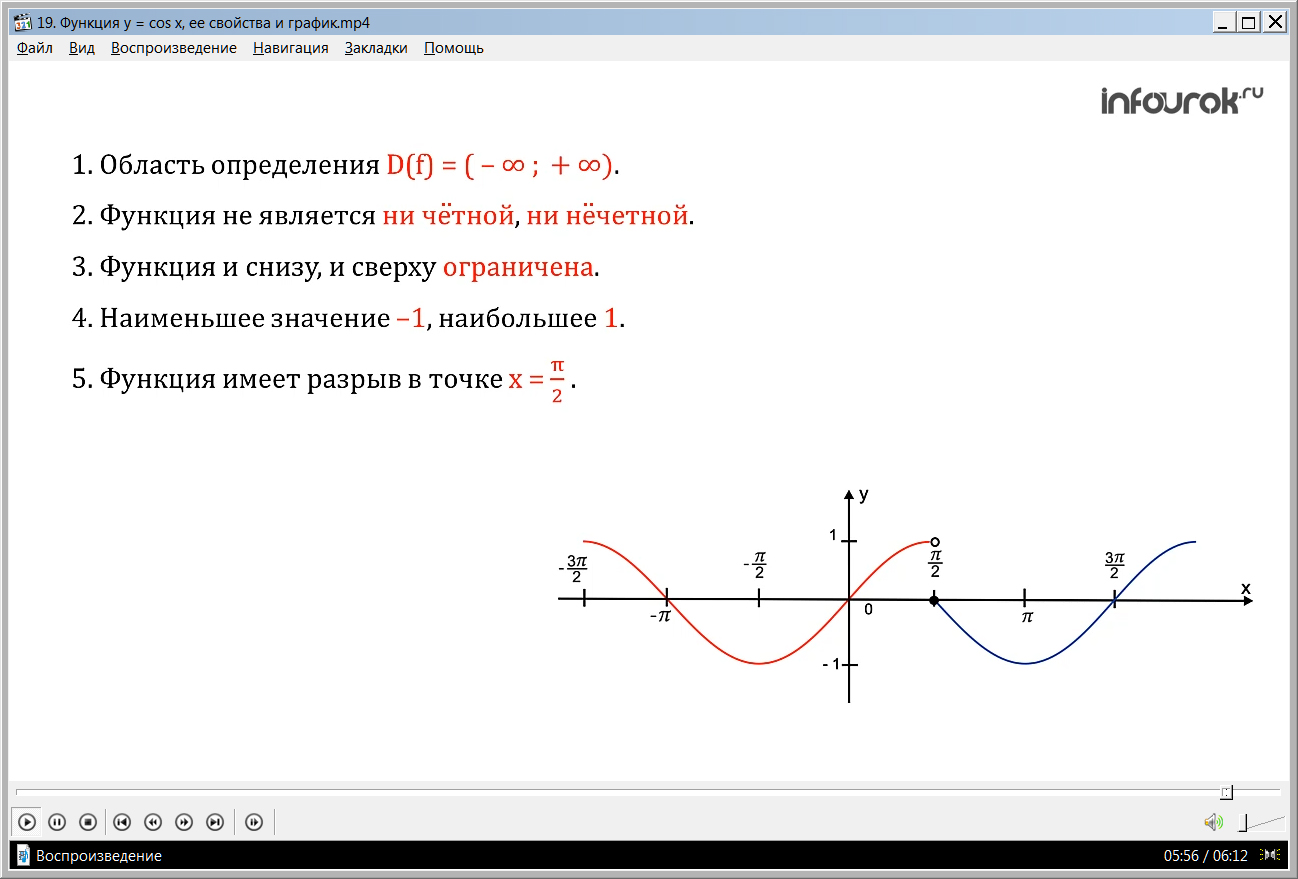
Прочитаем график этой функции (это значит перечислим свойства функции):
- Область определения – множество всех действительных чисел, т.е.
D(f) = ( - 14в€ћ ; + в€ћ)"> ( т.е. дэ от эф равно промежутку от минус бесконечности до плюс бесконечности).
- Функция не является ни четной, ни нечетной.
- Функция и снизу, и сверху ограничена.
- Наименьшее значение функции равно минус один ( таких точек бесконечно много) , наибольшее значение функции равно единице( таких точек тоже бесконечно много) .
- Функция имеет разрыв в точке х = 14ПЂ 2"> .
- Множеством значений функции является отрезок от минус единицы до единицы.
Читайте также: