Как из кос найти тангенс

Опубликовано: 17.09.2024

Как найти тангенс через косинус
Как найти тангенс, если известен косинус
Как найти синус, косинус и тангенс

косинус через тангенс формула

Как посчитать тангенс
Как найти котангенс угла
Что такое тангенс угла

Как найти тангенс внешнего угла
Как найти тангенс угла
Как выразить синус через косинус
Как решать тригонометрические функции
Как вычислить тангенс угла
Как найти тангенс угла в треугольнике
Как вычислить тангенс
Как посчитать котангенс
Как найти угол, если известен синус
Как решить задачи с косинусами
Как найти сторону через синус
Как найти синус внешнего угла
Как найти синус угла по сторонам треугольника
Как найти синус острого угла
Как найти гипотенузу, зная катет и угол
Как найти тангенс угла наклона
Как найти угол, если известен его тангенс
Как найти неизвестный катет
Как вычислить косинус
Что такое синус и косинус
Как найти косинус, зная синус
Как вычислить косинус угла

Внимание! Эти формулы работают только если аргументы у тригонометрических функций одинаковые, т.е.

\(sin^2⁡ 776^° +cos^2⁡ 776^° =1\)
\(tg\, 3x\cdot ctg\, 3x=1\)

\(sin^2⁡x+cos^2⁡3x≠1\)
\(tg\, x\cdot ctg\, y≠1\)

Все формулы связи тригонометрических функций учить не надо, потому что они достаточно легко получаются друг из друга несложными преобразованиями (подробности в этих видео). Кроме того, при частом использовании они постепенно запоминаются сами.

Примеры применения формул связи

Зачем нужны формулы связи? Они позволяют найти все тригонометрические функции угла, если известна лишь одна из них, а также дают возможность упрощать выражения, доказывать тождества, решать тригонометрические уравнения , заменяя одну функцию другой и так далее.

Пример. Найдите \(5sin⁡\,α\), если \(cos\,⁡α=\frac<2\sqrt<6>><5>\) и \(α∈(\frac<3π><2>;2π)\).
Решение. Нам известен косинус, найти надо синус. А что связывает синус и косинус? Основное тригонометрическое тождество:

Подставим вместо косинуса его значение:

Внимание! Последняя строчка – место, где теряется огромное количество баллов на ЕГЭ! Это одна из самых популярных ошибок – забыть отрицательный корень. Пожалуйста, раз и навсегда запомните, что у неполного квадратного уравнения вида \(x^2=a\) (при \(a>0\)) два корня \(x_1=\sqrt\) и \(x_2=-\sqrt\). Пусть двойка над иксом (та которая «квадрат») будет вам вечным маяком, сигнализирующим: «тут ДВА корня! Два! Не забудь!»

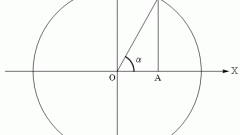
Вернемся к задаче. Получилось, что синус может иметь значение \(\frac<1><5>\) , а может \(-\) \(\frac<1><5>\) . И какое значение нам надо выбрать - с минусом или плюсом? Тут нам на помощь приходит информация, что \(α∈(\frac<3π><2>;2π)\). Давайте нарисуем числовую окружность и отметим отрезок \((\frac<3π><2>;2π)\).

Обратите внимание – в этой четверти синус принимает только отрицательные значения (можно провести перпендикуляры до оси синусов и убедиться, что это так).

Значит, в нашем случае \(sin\,⁡α=-\frac<1><5>\) т.е. \(5sin\,⁡α=5\cdot(-\frac<1><5>)=-1\).

Пример.Найдите \(tg\,α\), если \(cos\,⁡α=\) \(\frac<\sqrt<10>><10>\) и \(α∈(\frac<3π><2>;2π)\).
Решение. Есть 2 пути решения этой задачи:

- напрямую вычислить тангенс через формулу \(tg^2α+1=\) \(\frac<1>\) ;
- сначала с помощью тождества \(sin^2⁡α+cos^2⁡α=1\) найти \(sin⁡\,α\), а потом через формулу \(tg\,α=\) \(\frac\) получить тангенс.

В учебниках обычно идут первым путем, поэтому мы пойдем вторым.

Теперь вычислим косинус по упомянутой выше формуле:

Опять перед нами стоит выбор плюс или минус. Отметим отрезок \((\frac<π><2>;π)\) на тригонометрической окружности и посмотрим какие значения принимает косинус в этой четверти, чтобы определится со знаком.

Очевидно, что косинус отрицателен в этой четверти, а значит \(cos\,⁡α=-\) \(\frac<4><5>\) .

Осталось найти синус:

Опять используем круг, чтобы определить знак.

Пример (ЕГЭ). Найдите \(tg^2 α\), если \(5 sin^2⁡α+13 cos^2⁡α=6\).
Решение. Давайте пойдем от того, что известно. В равенстве \(5 sin^2⁡α+13 cos^2⁡α=6\) синус заменим на косинус:

Поняли почему именно синус заменили на косинус, а не наоборот? И почему не надо извлекать корень, досчитывая до «чистого» косинуса? Потому что для нахождения \(tg^2α\) хорошо подходит формула \(tg^2α+1=\) \(\frac<1>\) :

Теперь еще одна задача из ЕГЭ, для наглядности мы ее решение оформили картинкой.

Пример. Упростите выражение \(\frac<1>\) \(-ctg^2 α-cos^2 β\).
Решение.

Самое очевидное, что можно сделать – это представить котангенс как отношение косинуса к синусу.

Приводим дроби к общему знаменателю.

\(1-cos^2⁡α\) можно заменить на \(sin^2 α\).

Как найти тангенс угла, если известен косинус?

Как найти котангенс угла, если известен косинус?

Итак, читаем внимательно условие вопроса, и вспоминаем, чему нас учили в школе, у нас есть косинус угла, и этого окажется вполне достаточным для того, чтобы мы выполнили задание автора вопроса и нашли тангенс и котангенс данного угла. Вспоминаем, что мы можем найти, зная косинус, конечно-же, мы сразу можем найти синус, это очень легко, и в этом нам поможет вот это волшебное тождество и то, что из него следует, - формула для нахождения синуса:

Теперь, зная чему равен синус угла, через косинус, проще простого решать дальше по известным формулам для нахождения тангенса и котангенса, просто подставляя в них эти формулы для синуса, которые я разместила выше:

Для того, чтобы найти тангенс и котангенс через косинус, достаточно вспомнить тригонометрические формулы:

tgα = sinα / cosα.

ctgα = cosα / sinα.

Так как косинус известен, то синус можно найти из основного тригонометрического тождества:

sinα = √(1 - cos²α), если угол α находится в 1 и 2 четверти.

sinα = - √(1 - cos²α), если угол α находится в 3 и 4 четверти.

tgα = ± √(1 - cos²α) / cosα.

ctgα = ± cosα / √(1 - cos²α).

Так как произведение тангенса и котангенса = 1, то ctgα также можно найти из формулы: ctgα = 1 / tgα.

Пример

Косинус угла α равен 0,94, при этом α находится в 1 четверти (0

tg а = Sin a/Cos a. Чтобы выразить тангенс через косинус осталось выразить синус через косинус. Для этого воспользуемся основной тригонометрической формулой (Sin a)^2 +/(Cos a)^2 = 1. Тогда (Sin a)^2 = 1 - (Cos a)^2, Sin a = √(1 - (Cos a)^2), а tg = √(1 - (Cos a)^2)/Cos a. Например, при а= 60 градусов Cos 60° = 0,5, tg = √(1 - 0,25)/0,5 = √(0,75)/0,5 = √(3*0,25)/0,5 = (0,5*√3)/0,5 = √3 = 1,732. . ctg a = Cos a/Sin a, то-есть величина обратная tg а, и при а = 60° ctg 60° = 1/√3 = √3/3 = 0,57735. .

Первым делом стоит вспомнить определение тангенса и котангенса, а именно:

То есть получаются следующие формулы:

tg(x) = sin(x) / cos(x)

ctg(x) = cos(x) / sin(x)

Из условия задачи нам известен косинус, значит нам нужно будет найти синус. Для этого есть такая формула:

sin^2(x) + cos^2(x) = 1

Значит: sin^2(x) = 1 - cos^2(x)

sin(x) = √(1 - (Cos a)^2)

Теперь у нас есть значения синуса и косинуса, которые можно будет подставить в следующие формулы:

Наверное все помнят основное тождество тригонометрии: sin^2(x)+cos^2(x)=1. Почему-то также чётко я запомнил следующие простые формулы: tg^2(x)+1=sec^2(x) и ctg^2(x)+1=cosec^2(x). Ну и три определения: sec(x)=1/cos(x), cosec(x)=1/sin(x) и ctg(x)=1/tg(x).

Теперь осталось выбрать нужные и применить.

Допустим, cos(x)=(√3)/2, тогда sec(x)=2/√3, sec^2(x)=4/3, tg^2(x)=1/3, tg(x)=1/√3, ctg(x)=√3.

Пусть cosa = 1/2, тогда tga^2 = 1/(cosa)^2-1, (tga)^2 =1/0,25 - 1 = 3, tga =корень квадратный из 3, (со знаком + или - в зависимости в какой четверти находится а).

ctga = 1/корень из 3.

Синус, косинус, тангенс и котангенс угла - это тригонометрические функции. Можно сказать, что все они связаны между собой. Часто для нахождения одной из этих функций при условии, что известна другая, приходится вспоминать основные тригонометрические равенства или тождества, а также определение самих этих понятий. Зная все перечисленное выше, несложно выразить одну функцию через другую.

Тангенс угла - это отношение синуса этого угла к его косинусу.

Котангенс угла - это отношение косинуса угла к его синусу.

Нам известен косинус, из основного тригонометрического тождества ( sin²α + cos²α = 1 ) выразим синус:

sinα = √(1 - cos²α) для α из 1 и 2 четвертей,

sinα = -√(1 - cos²α) для α из 3 и 4 четвертей.

Подставив формулу для синуса угла в формулу тангенса и котангенса, получим формулы для вычисления значений этих функций:

tgα = ± √(1 - cos²α) / cosα,

ctgα = ± cosα / √(1 - cos²α).

Котангенс, впрочем, можно вычислить путем попроще, вспомнив, что тангенс и котангенс - функции обратные, то есть ctgα = 1 / tgα. Подставляем в формулу значение тангенса и вычисляем котангенс.

О чем эта статья:

Связь между sin и cos одного угла

Вы уже наверняка знаете, что тождественный — это равный.

Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.

Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:

sin 2 α + cos 2 α = 1

Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.

Равенство tg 2 α + 1 = 1/cos 2 α и равенство 1 + сtg 2 α + 1 = 1/sin 2 α выводят из основного тождества, разделив обе части на sin 2 α и cos 2 α.

В результате деления получаем:

Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.

sin 2 α + cos 2 α = 1

Сумма квадратов синуса и косинуса одного угла тождественно равна единице.

Чтобы доказать тождество, обратимся к теме единичной окружности.

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.

Докажем тождество sin 2 α + cos 2 α = 1

Произвольный угол α, тогда cos α = x0 = ОB.

Если развернуть точку A на угол α, то точка A становится на место точки A₁.

По определениям:

Синус угла (sin α) — это отношение противолежащего катета к гипотенузе.
Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.

Это значит, что точка A₁ получает координаты cos α, sin α.

Опускаем перпендикулярную прямую A₁B на x0 из точки A₁.

Образовался прямоугольный треугольник OA₁B.

|OB| = |x|.
Гипотенуза OA₁ имеет значение, равное радиусу единичной окружности.

|OA₁| = 1.
Применяя полученное выражение, записываем равенство по теореме Пифагора, поскольку получившийся угол — прямой:

|A₁B| 2 + |OB| 2 = |OA₁| 2 .
Записываем в виде: |y| 2 + |x| 2 = 1 2 .

Это значит, что y 2 + x 2 = 1.
sin угла α = y
cos угла α = x
Вставляем данные угла вместо координат точек:

OB = cos α
A₁B = sin α
A₁O = 1

Получаем основное тригонометрическое тождество: sin 2 α + cos 2 α = 1.
Что и требовалось доказать.

Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:

sin α = ±
cos α = ±

Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.

Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.

Тангенс и котангенс через синус и косинус

Синус угла — это ордината y.
Косинус угла — это абсцисса x.
Тангенс угла — это отношение ординаты к абсциссе.
Котангенс угла — это отношение абсциссы к ординате.

Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.

tg α =
ctg α =

Исходя из определений:

tg α =
=
ctg α =
=

Это позволяет сделать вывод, что тригонометрические тождества

задаются sin и cos углов.

Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.

Отдельно стоит обратить внимание на то, что тригонометрические тождества

верны для всех углов α, значения которых вписываются в диапазон.

Например, выражение
применимо для любого угла α, не равного
+ π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.

применимо для любого угла α, не равного π * z, где z — это любое целое число.

Связь между тангенсом и котангенсом

Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.

Тождество записывается в следующем виде:
tg α * ctg α = 1.

Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.

Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.

tg α * ctg α = 1.

ctg α = x/y

Отсюда следует, что tg α * ctg α = y/x * x/y = 1

Преобразовываем выражение, подставляем

,
получаем:

Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.

Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.

Если в голове вашего ребенка бурлит тригонометрическая каша, и все формулы смешались в один нераспутываемый клубок — записывайтесь на бесплатный вводный урок математики в онлайн-школу Skysmart.

Наши преподаватели помогут навести в голове порядок и разложить все знания по полочкам. На уроках вас ждут интересные задачки и располагающая атмосфера, в которой совсем не страшно задавать вопросы и получать от занятий — максимум.

Тангенс и косинус, котангенс и синус

Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.

Эта связь становится очевидна, если взглянуть на тождества:

tg 2 α + 1 =

Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.

1 + ctg 2 α =

Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.

Вывести оба этих тождества можно из основного тригонометрического тождества:
sin 2 α + cos 2 α = 1.

Для этого нужно поделить обе части тождества на cos 2 α, где косинус не равен нулю.
В результате деления получаем формулу tg 2 α + 1 =
Если обе части основного тригонометрического тождества sin 2 α + cos 2 α = 1 разделить на sin 2 α, где синус не равен нулю, то получим тождество:
1 + ctg 2 α =
.
Отсюда можно сделать вывод, что тригонометрическое тождество tg 2 α + 1 =
применимо для любого угла α, не равного
+ π + z, где z — это любое целое число.
А тригонометрическое тождество 1 + ctg 2 α =
применимо для любого угла, не равного π * z, где z — это любое целое число.

Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.

Основные тригонометрические тождества

Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Тригонометрия в прямоугольном треугольнике

Тригонометрический круг

Основное тригонометрическое тождество

Таблица значений тригонометрических функций

Градусы и радианы

Формулы приведения

Теорема синусов

Расширенная теорема синусов

Теорема косинусов

Тригонометрические уравнения (10-11 класс)

Примеры решений заданий из ОГЭ

Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.

sin α = Противолежащий катет гипотенуза

Косинус угла – отношение прилежащего катета к гипотенузе.

cos α = Прилежащий катет гипотенуза

Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).

tg α = Противолежащий катет Прилежащий катет

Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).

ctg α = Прилежащий катет Противолежащий катет

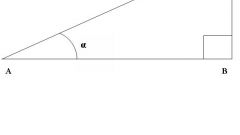
Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:

sin ∠ A = C B A B

cos ∠ A = A C A B

tg ∠ A = sin ∠ A cos ∠ A = C B A C

ctg ∠ A = cos ∠ A sin ∠ A = A C C B

sin ∠ B = A C A B

cos ∠ B = B C A B

tg ∠ B = sin ∠ B cos ∠ B = A C C B

ctg ∠ B = cos ∠ B sin ∠ B = C B A C

Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.

Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.

Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )

На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.

Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .

Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .

Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .

Рассмотрим прямоугольный треугольник A O B :

cos α = O B O A = O B 1 = O B

sin α = A B O A = A B 1 = A B

Поскольку O C A B – прямоугольник, A B = C O .

Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).

Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :

Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .

Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .

Координата по оси x – косинус угла , координата по оси y – синус угла .

Ещё одно замечание.

Синус тупого угла – положительная величина, а косинус – отрицательная.

Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .

Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .

sin 2 α + cos 2 α = 1

Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :

A B 2 + O B 2 = O A 2

sin 2 α + cos 2 α = R 2

sin 2 α + cos 2 α = 1

Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!

Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,

можно заметить, что:

sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °

sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °

sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °

sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °

cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °

cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °

cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °

cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °

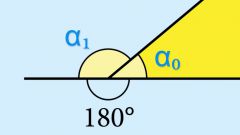
Рассмотрим тупой угол β :

Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:

sin ( 180 ° − α ) = sin α

cos ( 180 ° − α ) = − cos α

tg ( 180 ° − α ) = − tg α

ctg ( 180 ° − α ) = − ctg α

В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

a sin ∠ A = b sin ∠ B = c sin ∠ C

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A

b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B

c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C

Модуль геометрия: задания, связанные с тригонометрией.

Читайте также: